Determining signs (+/-/0) of derivatives from a polar graph

[d.tran103]

Homework Statement

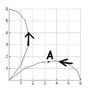
Use the polar graph to determine the signs (+,-,0) of each derivative at the point labeled A.

Homework Equations

dy/dx=
dy/dtheta=
dx/dtheta=
dr/dtheta=

The Attempt at a Solution

Hi people, I need help with this question. See the picture of the graph attached. I'm not sure if I'm over-complicating this question. I attempted to come up with the equation and got r=6cos2theta. I then substituted r=y/sintheta and r=x/costheta separately to eventually get my dy/dtheta and dx/dtheta, which eventually got dy/dx. I assumed that A came from theta=-2pi/3 and then I plugged that into get my answers. I ended up getting +, +, +, and -. However, my professor gave me the answers +,-,-, and -. Am I over-complicating the problem? Is there a way to just read the graph? Thanks!

 

[RoshanBBQ]

dy/dx is the easiest one. Just look at point A, then scoot forward a bit on the x-axis. We see that y grew a bit relative to y at point A. So dy/dx is positive. As for dy/dtheta, draw a radius line from the origin through point A. The angle this line makes with the x-axis is theta. So we scoot theta up a bit. We see that a new radius line going from the origin to a point very close to point A (such that theta increases) goes through a point with y less than y at A. So dy/dtheta is negative. Can you use this line of reasoning to figure out the remainder?

 

[d.tran103]

WOW! This makes sooooo much sense now. I understand it completely now. Thanks for taking your time to help me.