Benjamin_harsh
- 211
- 5
- Homework Statement
- why we need to add 180 to 56?
- Relevant Equations
- why we need to add 180 to 56?
The magnitude of each force is shown below:
F1 = 10 N
F2 = 20 N
F3 = 40 N
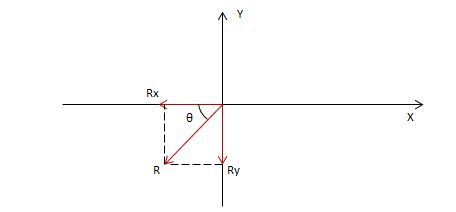
R = \sqrt {Rx^2 + Ry^2}
R = \sqrt {-10^2 -15^2} = 18N
θ = tan^{-1} \frac{Ry}{Rx}
θ = tan^{-1} \frac{Ry}{Rx} = 56
To express the direction of R, we need to calculate the direction angle (i.e. the counterclockwise angle that R makes with the positive x-axis), which in our case is 180° + θ, i.e. 236°.
why 236 but not 56? why we need to add 180 to 56?
F1 = 10 N
F2 = 20 N
F3 = 40 N
R = \sqrt {Rx^2 + Ry^2}
R = \sqrt {-10^2 -15^2} = 18N
θ = tan^{-1} \frac{Ry}{Rx}
θ = tan^{-1} \frac{Ry}{Rx} = 56
To express the direction of R, we need to calculate the direction angle (i.e. the counterclockwise angle that R makes with the positive x-axis), which in our case is 180° + θ, i.e. 236°.
why 236 but not 56? why we need to add 180 to 56?