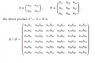Difference between direct sum and direct product

[Silviu]

Hello! I am reading something about applications of group theory in quantum mechanics and I got confused about the difference between direct sum and direct product. In many places I found that they mean the same thing. However, the ways I found them defined in the book I read from, seem to be different, even if they use the same mathematical symbol to represent the 2 of them. I attached the 2 ways they are defined in the book. So according to these definitions, if I understand it right, If A is 2x2 and B is 3x3, the direct sum will be 5x5 and the direct product will be 6x6, which are obviously not the same thing. So, can anyone explain this to me please? Thank you!

 

[fresh_42]

What is called a direct product here is misleading. It should better be named what it is: a tensor product.
A direct product and a direct sum are really often the same and are used to emphasize on the underlying structure. With additive structures like vector spaces, rings, algebras and here mappings one usually uses direct sum. On multiplicative structures like groups one may use direct product. The direct product can also be the cartesian product of sets. E.g.: Addition in a vector space $V$ is a function from the direct product $V \times V$ - here the cartesian product of pairs - onto $V$. And the direct sum $V \oplus V$ is the set of all pairs added: $V \oplus V = \{ u + v \, | \, u,v \in V\}$

Normally it is clear by the context it is used in.
However, the term direct product for a tensor product - only to distinguish between the direct sum of mappings and the tensor product - is rather unfortunate.