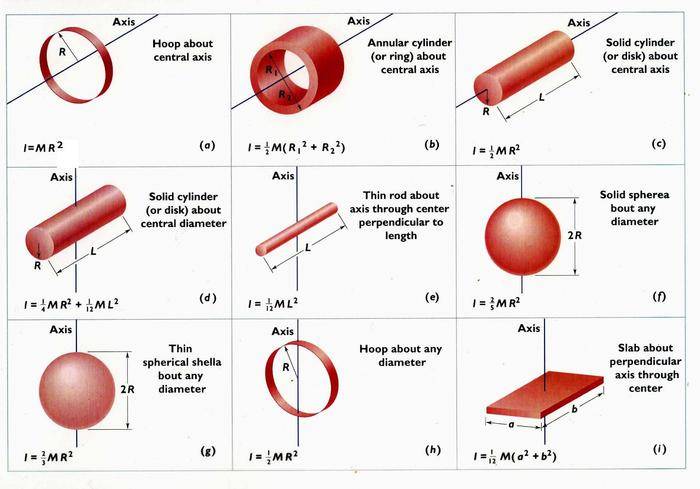
SUMMARY
The moment of inertia (I) is defined as I = MR^2 for a uniform ring, where M is mass and R is the distance from the axis of rotation. This formula applies specifically when each particle in the system is equidistant from the axis. For more complex shapes, such as solid cylinders, the moment of inertia can be derived using integration, specifically I_{net} = ∫ r^2 dm, where dm represents an infinitesimal mass element. The integration process involves defining mass density (ρ) and setting appropriate boundaries for the variables involved.
PREREQUISITES
- Understanding of basic physics concepts, particularly rotational dynamics.
- Familiarity with calculus, specifically integration techniques.
- Knowledge of mass density and its application in physics.
- Ability to interpret mathematical expressions related to physical formulas.
NEXT STEPS
- Study the derivation of moment of inertia for various geometric shapes, including spheres and rods.
- Learn about the application of the parallel axis theorem in calculating moment of inertia.
- Explore advanced integration techniques used in physics, particularly in rotational motion.
- Investigate real-world applications of moment of inertia in engineering and mechanical systems.
USEFUL FOR
Students of physics, mechanical engineers, and anyone interested in understanding rotational dynamics and the mathematical derivation of moment of inertia for different objects.