help
- 14
- 0
- Homework Statement
- help with my work
- Relevant Equations
- derivative and integral
Hello, good afternoon guys. I need a little help from you: D
1)n a positive integer.
f(x)=x(1-x)^n
Solve the equation f'(x)=0 in 0<x<1
this question I asked and found x = 1 / (x + 1) ok
2)An be the maximum value of f(x)=x(1-x)^n in [0,1]
Calculate lim (n+1)an
n tending to infinity
the maximum value would not be making the derivative equal to zero? would it be x = 1? I did not understand
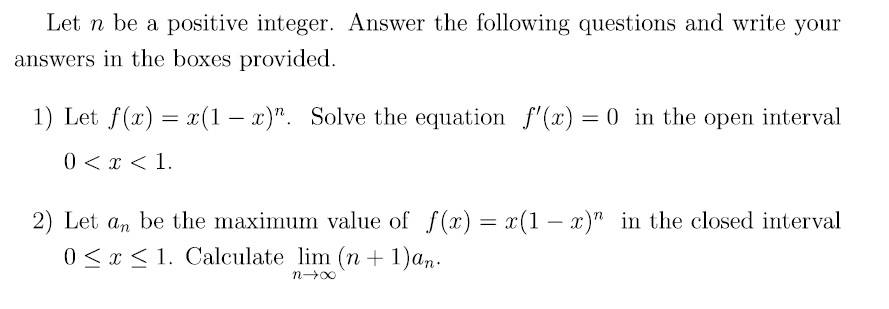
1)n a positive integer.
f(x)=x(1-x)^n
Solve the equation f'(x)=0 in 0<x<1
this question I asked and found x = 1 / (x + 1) ok
2)An be the maximum value of f(x)=x(1-x)^n in [0,1]
Calculate lim (n+1)an
n tending to infinity
the maximum value would not be making the derivative equal to zero? would it be x = 1? I did not understand
Last edited by a moderator: