- #1
zenterix
- 480
- 70
- Homework Statement
- Prove that the series
$$\sum\limits_{n=1}^\infty \frac{x}{n(1+nx^2)}\tag{1}$$
- Relevant Equations
- converges uniformly on ##\mathbb{R}##.
(Note that the above problem seems relatively straightforward and I think I solved it below. In post 3 is another problem also from Spivak's Calculus, and I haven't been able to solve that one).
Here is the solution I came up with
Consider the sequence of functions ##\{f_n\}=\left \{ \frac{x}{n(1+nx^2)}\right \}## defined on ##\mathbb{R}##.
By differentiating ##f_n(x)## and equating to zero we find critical points at ##x=\pm \frac{1}{\sqrt{n}}##.
By checking the second derivative we can see that these are the maximum and minimum of ##f_n##.
The absolute value of ##f_n## at these two points is the same: ##\frac{1}{2n^{3/2}}##.
Therefore, we can say that for all ##x\in\mathbb{R}## we have
$$|f_n(x)|\leq \frac{1}{2n^{3/2}}$$
Consider the sequence ##\{ M_n \}=\{\frac{1}{2n^{3/2}}\}##.
Then we can write that for all ##x\in\mathbb{R}## we have
$$|f_n(x)|\leq M_n$$
We can show that ##\{M_n\}## is summable by the integral test.
Therefore, by the Weierstrass M-test, the sequence ##\{f_n\}## is uniformly summable to the function ##f(x)=\lim\limits_{n\to\infty} (f_1+\ldots+f_n)## which is also denoted as ##\sum\limits_{n=1}^\infty f_n(x)##.
Here is my attempt at a more intuitive understanding of what is happening.
Here is a plot of ##f_1, f_2##, and ##f_3## in red, blue, and green, respectively.
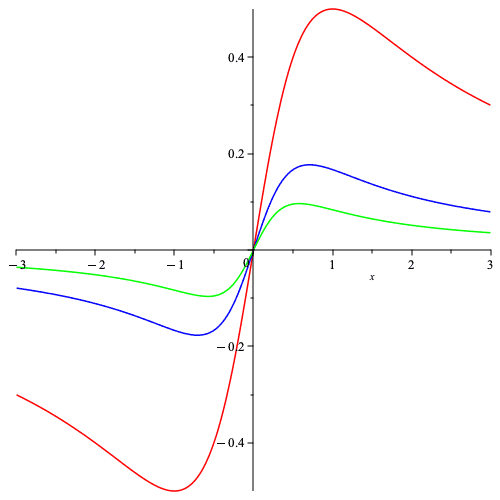
We can see that the sequence of maxima are decreasing and approach zero. In addition, the integral test shows that this sequence is summable.
Now, what we are interested in is the limit ##\lim\limits_{n\to\infty} (f_1+\ldots f_n)## which is a function that we denote as ##f(x)=\sum\limits_{n=1}^\infty f_n(x)##.
That is, we are summing graphs such as the three above plus infinite others.
By using the M-test, we ascertained that this sum converges uniformly to ##f##.
As far as I can tell, we don't know what this ##f## is exactly though, right?
Consider the sequence of functions ##\{f_n\}=\left \{ \frac{x}{n(1+nx^2)}\right \}## defined on ##\mathbb{R}##.
By differentiating ##f_n(x)## and equating to zero we find critical points at ##x=\pm \frac{1}{\sqrt{n}}##.
By checking the second derivative we can see that these are the maximum and minimum of ##f_n##.
The absolute value of ##f_n## at these two points is the same: ##\frac{1}{2n^{3/2}}##.
Therefore, we can say that for all ##x\in\mathbb{R}## we have
$$|f_n(x)|\leq \frac{1}{2n^{3/2}}$$
Consider the sequence ##\{ M_n \}=\{\frac{1}{2n^{3/2}}\}##.
Then we can write that for all ##x\in\mathbb{R}## we have
$$|f_n(x)|\leq M_n$$
We can show that ##\{M_n\}## is summable by the integral test.
Therefore, by the Weierstrass M-test, the sequence ##\{f_n\}## is uniformly summable to the function ##f(x)=\lim\limits_{n\to\infty} (f_1+\ldots+f_n)## which is also denoted as ##\sum\limits_{n=1}^\infty f_n(x)##.
Here is my attempt at a more intuitive understanding of what is happening.
Here is a plot of ##f_1, f_2##, and ##f_3## in red, blue, and green, respectively.
We can see that the sequence of maxima are decreasing and approach zero. In addition, the integral test shows that this sequence is summable.
Now, what we are interested in is the limit ##\lim\limits_{n\to\infty} (f_1+\ldots f_n)## which is a function that we denote as ##f(x)=\sum\limits_{n=1}^\infty f_n(x)##.
That is, we are summing graphs such as the three above plus infinite others.
By using the M-test, we ascertained that this sum converges uniformly to ##f##.
As far as I can tell, we don't know what this ##f## is exactly though, right?
Last edited: