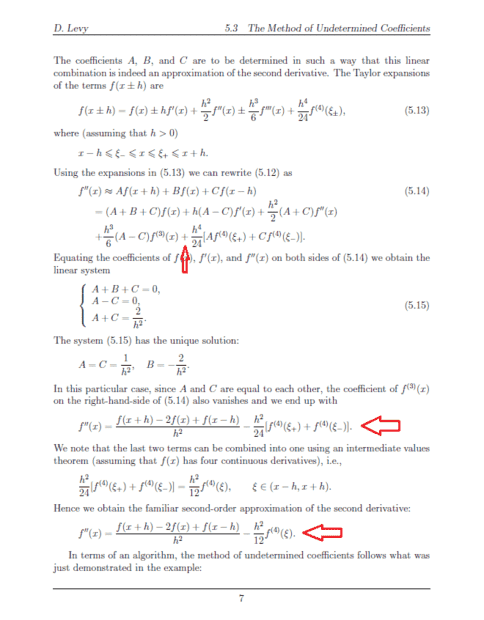Discussion Overview
The discussion revolves around a potential typo in differentiation formulas related to error terms in Taylor series. Participants are examining the implications of a sign change in an error term after substituting positive values.
Discussion Character
- Debate/contested, Conceptual clarification
Main Points Raised
- One participant questions whether the sign change in the error term from positive to negative is a typo or if there is a theoretical explanation for it.
- Another participant notes that the third term of a referenced equation is f”(x), suggesting it may be acceptable to have either a positive or negative value.
- A later post summarizes the initial concern about the error term and connects it to the Taylor series, seeking clarification on whether this aligns with the original question.
- One participant suggests transferring a term from the right-hand side to the left-hand side of an equation, indicating a possible method to address the confusion.
- Another participant expresses that they have resolved their confusion regarding the notation used in the discussion.
Areas of Agreement / Disagreement
Participants do not appear to reach a consensus on whether the sign change is a typo or an intentional aspect of the theory. Multiple viewpoints and interpretations are present.
Contextual Notes
The discussion includes unresolved questions about the notation and the implications of the sign change in the error term, which may depend on specific definitions or contexts not fully articulated.