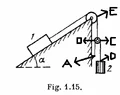
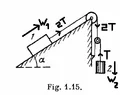
You could post this under homework. I looked more closely and those diagrams and it's a little complicated. Three suggestions:
1) You need to figure out how many degrees of freedom the system has. The weight can move down (or up); the pulley can move down (or up); and, then weight can move up the ramp (or down).
2) Consider a small displacement from the starting position. If the weight moves down ##\Delta y_W## and the pulley moves down ##\Delta y_P##, then you can figure out how much the weight must have moved ##\Delta x##. Note I'm using ##x## for the direction up the slope.
3) Consider using conservation of energy, rather than forces and tensions.
Note that if you have an equation involving displacements ##y_W, y_P## and ##x##, then you can differentiate that equation with respect to time and get an equation for the velocities ##v_W, v_P## and ##v_x##. Velocities are what are needed for the energy equation.
Alternatively, you could differentiate again to get an equation in the accelerations and relate this to the forces and tensions involved. But, from experience, I'd say energy is the way to go for a problem like this.