CGandC
- 326
- 34
1. when writing a proof, I stumbled upon cases where I wondered if the following two are equivalent?:
a. " There exists ## n \in N ## such that ___ "
b. " Let ## n \in N ## be arbitrary such that ___"
Are these statements the same? Is ## n ## in both of them the same?
2. Suppose I have the following set
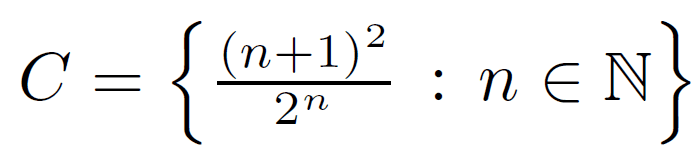
And I want to prove that there exists a real number ## m ## such that for all ## a \in C ## it is satisfied that ## a \leq m ##.
So writing of the proof goes as follows:
We'll take ## 2 \in R ##. Let ## b \in C ## , meaning there exists ## n \in N ## such that ## b = \frac{n+1}{2^n} ## . So we'll prove that ## \frac{n+1}{2^n} \leq 2 ## .
I saw in the answers that the proof of ## \frac{n+1}{2^n} \leq 2 ## is done with induction on ## n ##.
The question is: how is it possible to do proof by induction on ## n ## here if in the writing of the proof I said " there exists ## n \in N ## " and not " arbitrary ## n \in N ## " or " Let ## n \in N ## "?
I know that I do proof by induction if I have a claim such as ## \forall n \in N. P(n) ##. But here in the writing of the proof I have a claim of ## \exists n \in N. P(n) ## which I have to prove, which isn't the same as the previous claim.
a. " There exists ## n \in N ## such that ___ "
b. " Let ## n \in N ## be arbitrary such that ___"
Are these statements the same? Is ## n ## in both of them the same?
2. Suppose I have the following set
And I want to prove that there exists a real number ## m ## such that for all ## a \in C ## it is satisfied that ## a \leq m ##.
So writing of the proof goes as follows:
We'll take ## 2 \in R ##. Let ## b \in C ## , meaning there exists ## n \in N ## such that ## b = \frac{n+1}{2^n} ## . So we'll prove that ## \frac{n+1}{2^n} \leq 2 ## .
I saw in the answers that the proof of ## \frac{n+1}{2^n} \leq 2 ## is done with induction on ## n ##.
The question is: how is it possible to do proof by induction on ## n ## here if in the writing of the proof I said " there exists ## n \in N ## " and not " arbitrary ## n \in N ## " or " Let ## n \in N ## "?
I know that I do proof by induction if I have a claim such as ## \forall n \in N. P(n) ##. But here in the writing of the proof I have a claim of ## \exists n \in N. P(n) ## which I have to prove, which isn't the same as the previous claim.