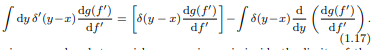Discussion Overview
The discussion revolves around the properties and interpretations of the Dirac delta function when integrated over a finite interval, specifically addressing different cases of integration limits and the implications of those cases. Participants explore theoretical aspects, mathematical reasoning, and potential applications related to the delta function.
Discussion Character
- Debate/contested
- Mathematical reasoning
- Conceptual clarification
Main Points Raised
- Some participants question whether the integral of the Dirac delta function over the interval \([-1, 1]\) should yield 1 for \(-1 \leq x_0 \leq 1\) or for \(-1 < x_0 < 1\).
- One participant argues that the first case leads to contradictions when considering integrals over larger intervals, suggesting that the second case may be more appropriate.
- Another participant introduces the idea that by symmetry, the integral of the delta function over \([0, 1]\) should equal \(\frac{1}{2}\), proposing a different interpretation of the delta function at the boundaries.
- There is a reference to a definition of the functional derivative and its relation to the delta function, with some participants expressing uncertainty about the manipulations involving derivatives of the delta function.
- Participants share personal experiences with learning materials and express varying levels of confidence in their understanding of the topic, indicating a mix of familiarity and uncertainty.
- Links to external lecture notes are provided, suggesting additional resources for understanding the delta function and its applications.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the correct interpretation of the integral of the Dirac delta function over the specified interval. Multiple competing views remain regarding the treatment of boundary cases and the implications of symmetry.
Contextual Notes
Some participants note that their understanding is influenced by specific examples and definitions from literature, which may not be universally accepted. There are references to potential typos and missing elements in mathematical expressions, indicating that the discussion is still evolving.
Who May Find This Useful
This discussion may be of interest to students and professionals in physics and mathematics, particularly those exploring the properties of distributions, functional derivatives, and the Dirac delta function in theoretical contexts.