Dirac Delta using Fourier Transformation

[arpon]

We know,
$$\delta(x) = \begin{cases}
\infty & \text{if } x = 0 \\
0 & \text{if } x \neq 0
\end{cases}$$
And, also,
$$\int_{-\infty}^{\infty}\delta(x)\,dx=1$$
Using Fourier Transformation, it can be shown that,
$$\delta(x)=\lim_{\Omega \rightarrow \infty}\frac{\sin{(\Omega x)}}{\pi x}$$
Let's look at the graph of $y=\frac{\sin{(\Omega x)}}{\pi x}$, for large $\Omega$.

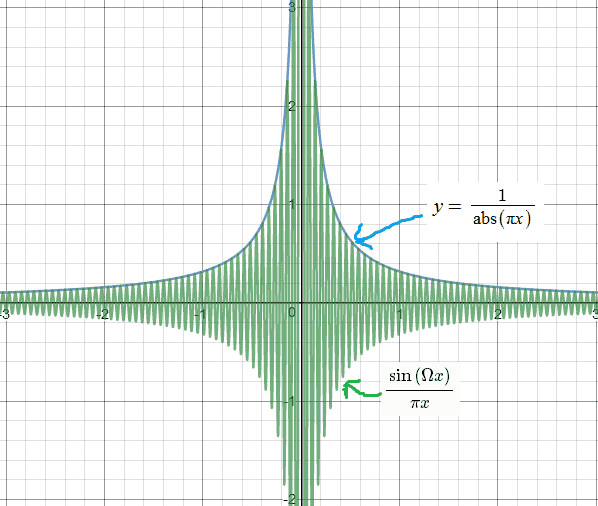
So, from this graph, it seems,
$$\lim_{\Omega \rightarrow \infty}\frac{\sin{(\Omega x)}}{\pi x}\neq 0 \text{ , for } x\neq 0 $$

But, this is actually the Fourier transformation of the function,
$$f(t)=1=\exp{(i\cdot 0\cdot t)}$$

So, intution tells me that the frequency spectrum of $f(t)$ should have infinite amplitude at $x=0$ and $0$ amplitude otherwise, just like the Dirac-delta function.

Now, how can I show that,
$$\lim_{\Omega \rightarrow \infty}\frac{\sin{(\Omega x)}}{\pi x} = 0 \text{ when, } x\neq 0$$

 

[Delta2]

The rigorous definition of dirac delta function is not the one you write at the beginning of your post. Even if we accept that definition (because intuitively that's what the dirac delta is) then I don't know how you come up with $\delta(x)=\lim_{\Omega \rightarrow \infty} \frac{sin(\Omega x)}{\pi x}$ cause that limit simply does NOT exist. (it does not exist for $x\neq 0$, if we first take the limit x->0 then it exists and is infinite).

 

[arpon]

The rigorous definition of dirac delta function is not the one you write at the beginning of your post. Even if we accept that definition (because intuitively that's what the dirac delta is) then I don't know how you come up with $\delta(x)=\lim_{\Omega \rightarrow \infty} \frac{sin(\Omega x)}{\pi x}$ cause that limit simply does NOT exist. (it does not exist for $x\neq 0$, if we first take the limit x->0 then it exists and is infinite).

Using Fourier transformation, we have,

Comparing with the equation,
$$f(t)=\int_{-\infty}^{\infty}\delta(t-u)f(u)\,du$$
we have,

Thus,
$$\begin{align}
\delta(t)&=\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{i\omega t}\,d\omega\\
&=\frac{1}{2\pi}\lim_{\Omega\rightarrow \infty}\left[\frac{e^{i\omega t}}{i\omega t}\right]^{\Omega}_{\omega=-\Omega}\\
&=\lim_{\Omega \rightarrow \infty}\frac{\sin{(\Omega t)}}{\pi t}
\end{align}$$

Reference:
Mathematical Methods for Physics and Engineering: A Comprehensive Guide, 3rd Edition by K. F. Riley, M. P. Hobson, S. J. Bence, Page/442

 

[Delta2]

The last two equalities would hold only if the limit $\frac{1}{2\pi}\lim_{\Omega\rightarrow \infty}\left[\frac{e^{i\omega t}}{it}\right]^{\Omega}_{\omega=-\Omega}= \lim_{\Omega \rightarrow \infty}\frac{\sin{(\Omega t)}}{\pi t}$ existed but it does not exist, as you can easily prove for any x<>0 the limit $\lim_{\Omega \rightarrow \infty}\sin{(\Omega x)}$ does not exist.