Direct Modulation and Photon Lifetime - Laser

[ulver48]

Hello,

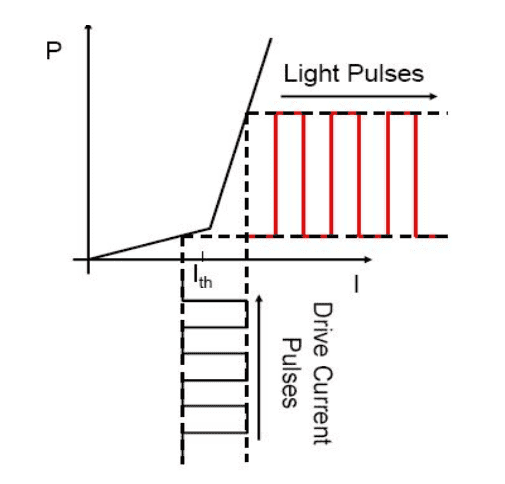
There is a thing I struggle to understand on laser physics. There is a modulation method called direct modulation for semiconductor lasers where by changing the current we modulate the light which is emitted form the laser cavity. There is a picture below

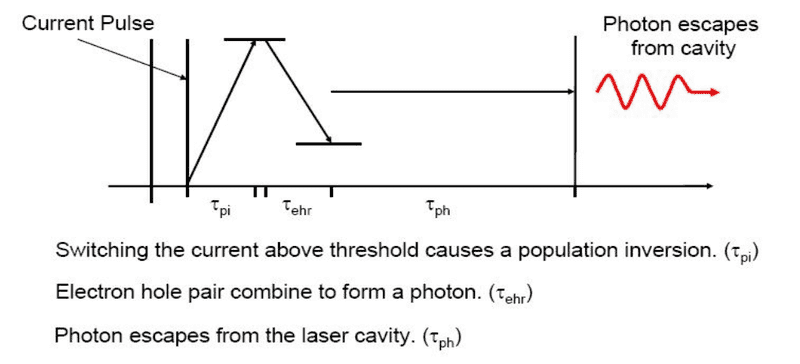
It is stated in bibliography that the fundamental limit as far as the modulation frequency is concerned is the inverse of the photon lifetime. This is shown in the following picture. Can someone explain to me why tph is the fundamental limit? Thank you for your time.

 

[mfb]

If you cut off the power "instantly", you still have the population inversion - the laser will continue to emit photons until most atoms are in the ground state again. The time is related to the photon lifetime.
If you switch on the power "instantly", you first have to excite enough atoms to reach population inversion before the laser starts working. Typically the time constant here will be similar.

 

[ulver48]

So you can't understand this concept just by imagining that the photon is a particle bouncing back and forth in the laser cavity until it abandons it. You take the rate equations of the laser and you find the time needed for the population inversion to happen in order for the stimulated emission rate to be higher than the absorption rate. So if you modulate the laser so as to create population inversion and then you cut off the current immediately, you will see a small portion of coherent light coming out of the laser cavity and then immediately absorption and spontaneous emissions will become greater than the stimulated emission and you will see no coherent light afterwards. Isn't then the fundamental limit equal to the turn on delay? Is this turn on delay related to the photon lifetime? From the above diagram the turn on delay is equal to τ_pi, not τ_ph. I am a little confused.

Edit: No I am wrong. It is not only the turn on delay. The photons must have time to destabilize some electrons on the higher level and create some coherent light. I remember that this time is equal to the time needed for a round trip. But a photon can make many round trips before it is gone. Well yes, shouldn't the round trip time be the fundamental limit ?

Edit2: Oh , I see it now. The photon must have also sometime...well to escape the cavity. If the population is not maintained long enough then absorption will get the poor photons and no coherent light will come out of the laser. Was it that simple ?