Discontinuities in a Poincare map for a double pendulum

[eddy_purcell]

I'm generating poincare sections of a double pendulum, and they mostly look okay, but some of them have weird discontinuities that seem wrong.
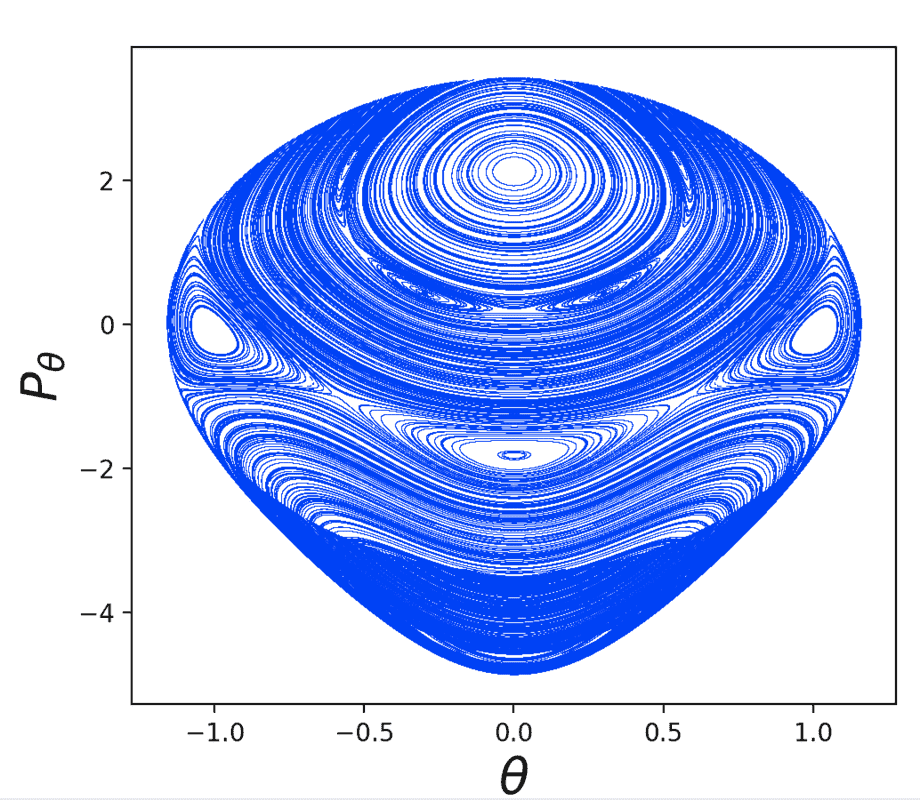
The condition for these sections is the standard $\theta_1 = 0$ and $\dot{\theta}_1 > 0$. Looking at one of the maps, we see that most of the sections look fine, but there are some weird intersections in the bottom:

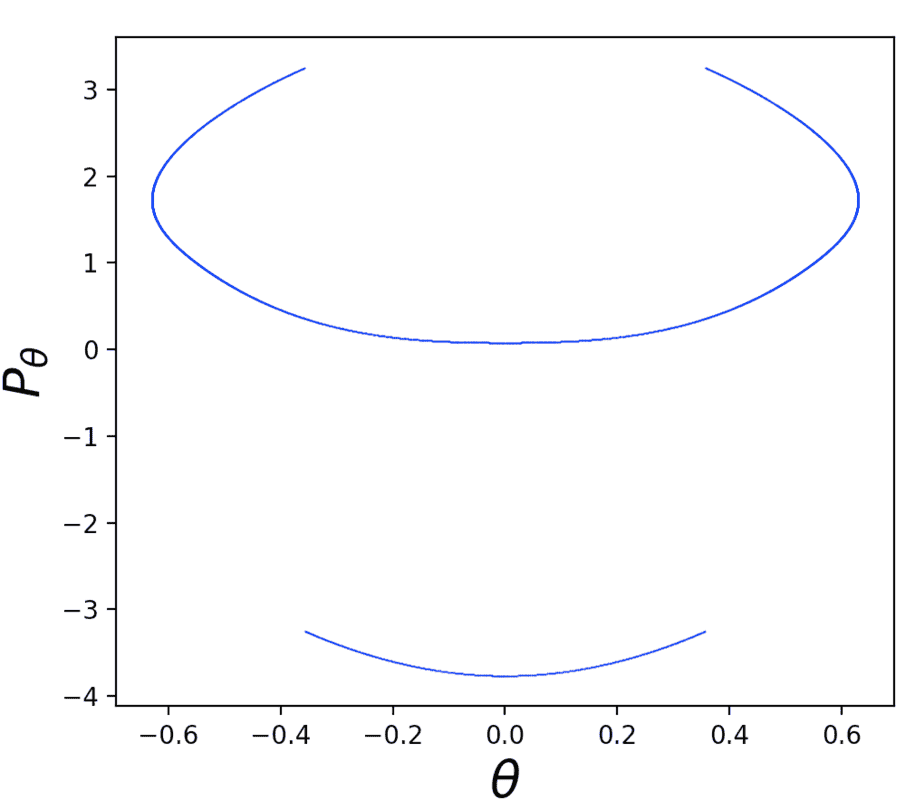
If we look at just one of these sections, we see that the top part is being flipped upside down:

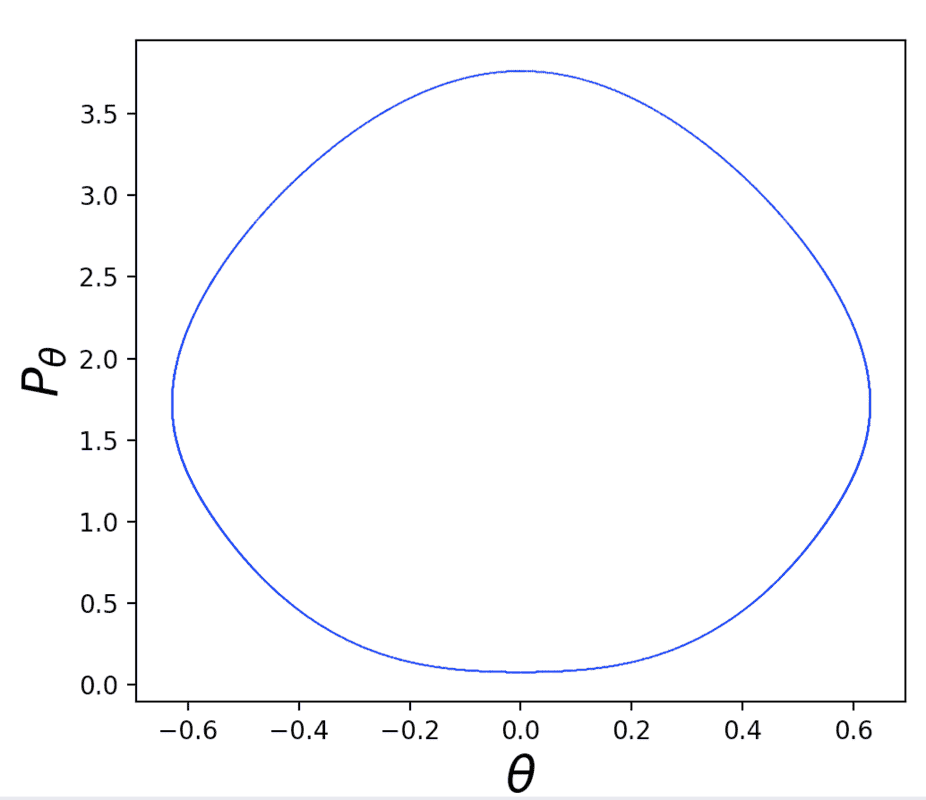
Indeed, if we just multiply the bottom bit by $−1$, it looks just fine:

This is weird, right? None of the analogous plots I've seen in the literature look like this; they all have symmetric limits along the vertical axis.

The fact that the other sections seem fine makes me think that I transposed the equations correctly, but this problem has been extremely frustrating to diagnose. I've been able to figure out that all of the affected sections are those whose initial condition required $\dot{\theta}_1<0$ in order to get a condition with the correct total energy, but I have no idea why that would make them look like this.

Any ideas about what I'm missing?

 

[Ibix]

Looks like it's happening at $\dot\theta=\pi$. My guess would be that one of your inverse trig functions believes in angles in the range $-\pi \rightarrow \pi$, while you believe them to lie in $0\rightarrow 2\pi$.

 

[eddy_purcell]

Looks like it's happening at $\dot\theta=\pi$. My guess would be that one of your inverse trig functions believes in angles in the range $-\pi \rightarrow \pi$, while you believe them to lie in $0\rightarrow 2\pi$.

Interesting idea, and I'll look into it, but I think that that was just a coincidence. Taking another one of the problematic sections, we see that it occurs lower down: