Displacement-Time Graph Velocity of Objects X & Y

[mathlearn]

View attachment 6152

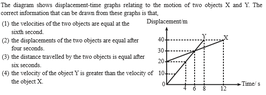
The gradient of the displacement time graph is the velocity.

Gradient of x = $\frac{y_1-y_2}{x_1-x_2}=\frac{30-40}{6-12}=\frac{-10}{-6}=\frac{5}{3}$ meters per second

Gradient of y = $\frac{y_1-y_2}{x_1-x_2}=\frac{0-40}{0-8}=\frac{-40}{-8}=5$ meters per second

Therefore the first option is false the second is also so not true, according to my calculations above the fourth option is true,and also it looks like the third is also true as the displacement is equal

Many Thanks :)

 

[Evgeny.Makarov]

I agree with you on (1), (2) and (4). Concerning (3), displacements are indeed equal at $t=6$. According to Wikipedia, displacement is the difference between the final and initial position vectors. In this problem, apparently, objects move along a line, so instead of vectors we may consider their position $s(t)$ at time $t$ on the line. Suppose displacement is counted relative to some initial time $t_0$. ($t_0$ cannot be 0 because $s_X(0)-s_X(t_0)=20$.) So
\begin{align}
s_X(6)-s_X(t_0)&=30\\
s_X(0)-s_X(t_0)&=20,
\end{align}
from where $s_X(6)-s_X(0)=10$. Similarly, $s_Y(6)-s_Y(0)=30$. The graph shows that the objects did not change the direction, so the distance $X$ traveled between $t=0$ and $t=6$ equals $|s_X(6)-s_X(0)|=10$, while the distance $Y$ traveled is 30.