Divide a line segment into three equal parts

  • Context: MHB 
  • Thread starter Thread starter Amer
  • Start date Start date
  • Tags Tags
    Line parts
Click For Summary

Discussion Overview

The discussion revolves around the question of whether it is possible to divide a line segment into three equal parts using only a compass and ruler. Participants explore various methods and address the related topic of angle trisection, as well as the implications of mathematical proofs regarding these constructions.

Discussion Character

  • Exploratory
  • Technical explanation
  • Debate/contested
  • Mathematical reasoning

Main Points Raised

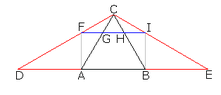
  • Some participants assert that it is indeed possible to trisect a line segment using specific geometric constructions involving rays and parallel lines.
  • Others clarify that the impossibility of trisection is often associated with angle trisection, which cannot be achieved with a straightedge and compass alone.
  • A participant describes a method involving the construction of an equilateral triangle to facilitate the division of the line segment into three equal parts.
  • There are repeated inquiries about how to construct a 60-degree angle using an unmarked straightedge and compass, with differing opinions on the feasibility of such constructions.
  • Some participants express skepticism about the methods proposed, suggesting that certain constructions cannot be performed as described.

Areas of Agreement / Disagreement

The discussion reveals multiple competing views on the methods for trisecting a line segment, with no consensus reached on the validity of the proposed techniques or the impossibility of certain constructions.

Contextual Notes

Participants reference mathematical proofs and concepts from abstract algebra, indicating that the discussion may depend on specific definitions and assumptions regarding geometric constructions.

Amer
Messages
259
Reaction score
0
is there a way to divide a line segment into three equal parts using just compass and ruler ?
I heard that there is not a way and there is a proof for that is that right ?
 
Mathematics news on Phys.org
Re: divde a line segment into three equal parts

Amer said:
is there a way to divide a line segment into three equal parts using just compass and ruler ?
I heard that there is not a way and there is a proof for that is that right ?

It is possible. Draw a line segment AB. draw a ray beginning at A at an angle of 60 degrees to AB. draw another ray beginning at B at an angle of 60 degrees from BA(Note that the second ray is in opposite direction of first ray). Take any arbitrary distance on the compass. Put pointy end of compass on point A and cut first ray at point K. put pointy end of compass on K and cut first ray again to get point L. Put pointy end of compass on B and cut second ray to get point M and now put pointy end of compass on M and cut second ray to get point N. join KN and LM. The line segment AB is now trisected.
 
Re: divde a line segment into three equal parts

Perhaps you're thinking of an angle trisection instead of a line trisection? It is true that the angle cannot, so far as we know, be trisected using straightedge and compass.
 
Re: divde a line segment into three equal parts

Amer said:
is there a way to divide a line segment into three equal parts using just compass and ruler ?
I heard that there is not a way and there is a proof for that is that right ?
Angles, in general, cannot be trisected using (unmarked)straight edge and compass alone. In "Abstract Algebra" texts, example Herstein's "Topics in Algebra", it is proved that and 60 degree cannot be trisected using unmarked straight edge and compass alone.
 
Re: divde a line segment into three equal parts

how to draw an angle of 60 ? with straight ruler unmarked with compass
that can't be done
 
Re: divde a line segment into three equal parts

Amer said:
is there a way to divide a line segment into three equal parts using just compass and ruler ?
I heard that there is not a way and there is a proof for that is that right ?
We can divide any line segment into any finite natural number of congruent sub-segments.
Start with $\overline {AB} $. At $A$ draw any ray not collinear with $\overrightarrow {AB}$.
Now on that ray starting at $A$ mark off three points $E,~F,~\&~G$ so that $\overline {AE},~\overline {EF},~\&~\overline {FG}$ have the same length.
Join $G~\&~B$ with a line. Construct at $E~\&~F$ lines parallel $\overline {GB}$.
Those lines will trisect $\overline {AB}$.
 
Re: divde a line segment into three equal parts

The segment AB that must divide into three parts is represented in the figure...

View attachment 131

The following procedure requires only a non graduaded rule and a compass...

a) construct the equilateral triangle ABC...

b) construct the segments DA=AB and BE=AB collinear to AB...

c) draw the segments DC and CE...

d) draw vertical lines passing through A and B a call F and I the intersection point with the segments DC and CE...

e) draw the horizontal segment FI and call G and H the intersection points with the segments AC and BC...

At this point we have the segment FI that is equal to AB and is divided into three equal segments FG, GH and HI...

Kind regards

$\chi$ $\sigma$
 

Attachments

  • MHB11.PNG
    MHB11.PNG
    988 bytes · Views: 138
Re: divde a line segment into three equal parts

Amer said:
how to draw an angle of 60°? with straight ruler unmarked with compass
that can't be done

Draw an equilateral triangle with unmarked straight ruler and compass. Then you even have got three angles with 60°.
 
Re: divde a line segment into three equal parts

thank you all,thats great :D
 
  • #10
Re: divde a line segment into three equal parts

Amer said:
how to draw an angle of 60 ? with straight ruler unmarked with compass
that can't be done
It surely can be done. Use the ruler to draw a straight line. Mark any two points on the line and call them "A" and "B". Using the compass strike a circle through "B" having center "A". Using the compass strike a circle through "A" with center "B". Those circles with intersect in two points. Choose either of them and call it "C". The angle CAB will have measure 60 degrees.
 

Similar threads

High School Constructing a Line Segment Equal to a Circle's Circumference?
  • · Replies 6 ·
Replies
6
Views
2K
MHB Dividing Line Segments into Four Equal Parts using Midpoint Formula
  • · Replies 5 ·
Replies
5
Views
2K
High School Calculate distance between ends of a circle segment
  • · Replies 22 ·
Replies
22
Views
3K
High School A Simpler Way to Find the Shaded Area?
  • · Replies 1 ·
Replies
1
Views
2K
MHB Line Segment AB....Challenge Question
  • · Replies 12 ·
Replies
12
Views
3K
MHB Finding the Length of a Dividing Line in a Trapezoid
  • · Replies 5 ·
Replies
5
Views
2K
MHB How to divide a circumference into equal parts, WITHOUT COMPASS?
  • · Replies 1 ·
Replies
1
Views
3K
Undergrad How to obtain the inverse (reciprocal) of a line segment?
  • · Replies 13 ·
Replies
13
Views
3K
MHB How to Use the Midpoint Formula to Find the Other Endpoint of a Line Segment?
  • · Replies 9 ·
Replies
9
Views
2K
MHB Prove Quadrilateral Divider: Equal Area & Perimeter
  • · Replies 4 ·
Replies
4
Views
2K