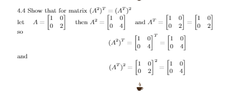MHB Does $(A^T)^2=(A^2)^T$ for $2\times 2$ matrices?

  • Thread starter Thread starter karush
  • Start date Start date
karush
Gold Member
MHB
Messages
3,240
Reaction score
5
View attachment 8980
this is a c/p from my overleaf DE hw

but on proving this I only used a $2\times 2$ matrix

Also I thot $A^2$ meant A(A) a composite but the calculators just multiplied it.typos maybe:rolleyes:
 

Attachments

  • 4.4.PNG
    4.4.PNG
    3.3 KB · Views: 118
Last edited:
Physics news on Phys.org
If you think of a matrix as an operator, then matrix multiplication is functionally equivalent to composition. Recall that $(AB)^T=B^T A^T,$ so that
$$\left(A^T\right)^2=A^TA^T=(AA)^T=\left(A^2\right)^T.$$
 

Thread 'Trouble understanding an online solution to an exercise in Dummit & Foote'

##\textbf{Exercise 10}:## I came across the following solution online: Questions: 1. When the author states in "that ring (not sure if he is referring to ##R## or ##R/\mathfrak{p}##, but I am guessing the later) ##x_n x_{n+1}=0## for all odd $n$ and ##x_{n+1}## is invertible, so that ##x_n=0##" 2. How does ##x_nx_{n+1}=0## implies that ##x_{n+1}## is invertible and ##x_n=0##. I mean if the quotient ring ##R/\mathfrak{p}## is an integral domain, and ##x_{n+1}## is invertible then...
View full post »

Thread 'Questions about non existence of GCDs vs (coimages, cokernels)'

The following are taken from the two sources, 1) from this online page and the book An Introduction to Module Theory by: Ibrahim Assem, Flavio U. Coelho. In the Abelian Categories chapter in the module theory text on page 157, right after presenting IV.2.21 Definition, the authors states "Image and coimage may or may not exist, but if they do, then they are unique up to isomorphism (because so are kernels and cokernels). Also in the reference url page above, the authors present two...
View full post »

Thread 'Decomposition into irreps of compact Lie group'

When decomposing a representation ##\rho## of a finite group ##G## into irreducible representations, we can find the number of times the representation contains a particular irrep ##\rho_0## through the character inner product $$ \langle \chi, \chi_0\rangle = \frac{1}{|G|} \sum_{g\in G} \chi(g) \chi_0(g)^*$$ where ##\chi## and ##\chi_0## are the characters of ##\rho## and ##\rho_0##, respectively. Since all group elements in the same conjugacy class have the same characters, this may be...
View full post »

Similar threads

A The colorful world of ##2\times 2## complex matrices
Replies
7
Views
2K
I Show that ##\mathbb{C}## can be obtained as 2 × 2 matrices
Replies
14
Views
3K
I Proving SL_2(C) Homeomorphic to SU(2)xT & Simple Connectedness
Replies
1
Views
2K
I Congruence for Symmetric and non-Symmetric Matrices for Quadratic Form
Replies
7
Views
2K
MHB E2.3 Express T_b^b as the product of three matrices
Replies
2
Views
1K
MHB Gaussian Probability: 1 to 2 in tikz
Replies
7
Views
2K
I Orthogonal transformations preserve length
Replies
1
Views
2K
A The meaning of ##(ict, x_1,x_2,x_3)##
Replies
4
Views
2K
MHB Matrix Operations: Solving for A+B, AB, BA, AC, and CA
Replies
2
Views
1K
I How can I test for positive semi-definiteness in matrices?
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top