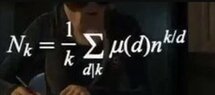Does anyone recognize this equation?
- Context: Graduate
- Thread starter ElliotSmith
- Start date
Click For Summary
SUMMARY
The equation discussed pertains to the Mobius Inversion function, specifically relating to the summation of all divisors d of k. It is confirmed that if n is a power of a prime number, the right side of the equation represents the count of monic irreducible polynomials of degree k over a finite field with n elements. This connection is explicitly detailed in the Algebraic number theory section of the Mobius inversion formula on Wikipedia.
PREREQUISITES- Understanding of Mobius Inversion function
- Familiarity with divisor summation
- Knowledge of finite fields
- Basic concepts of algebraic number theory
- Research the Mobius Inversion formula in detail
- Study the properties of monic irreducible polynomials
- Explore the applications of finite fields in algebra
- Learn about divisor functions and their significance in number theory
Mathematicians, students of number theory, and anyone interested in algebraic structures and polynomial theory will benefit from this discussion.
Similar threads
Undergrad
Relevance of an orphaned equation
- · Replies 14 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 5 ·
- · Replies 2 ·
- · Replies 11 ·
Undergrad
Trigonometry problem of interest
- · Replies 81 ·
- · Replies 6 ·
- · Replies 2 ·
- · Replies 1 ·