Dominant Feynman diagram for ##b \to s ~l^+ l^−##

[Safinaz]

Hi all,

It's written in QFT books, see for instance George_W._S. book "Flavor Physics and the TeV Scale" that the following Feynman diagram (1)

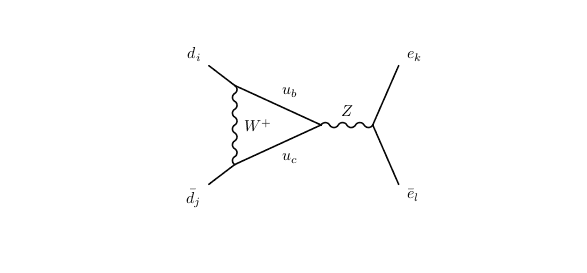
is the dominant Feynman diagram for $b \to s ~l^+l^−$ decay. Actually I compare this diagram via another possible diagram (2)

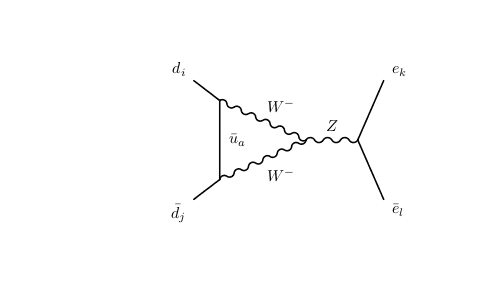
Both (1) and (2) are proportional to$G_F^2$, so they are on equal coupling order, also (1) proportional to

\begin{align}
\Big(\frac{1}{k\!\!/ - m_t}\Big)^2 ~ \frac{1}{k^2 - m_w^2},
\end{align}

while (2) proportional to

\begin{align}
\frac{1}{k\!\!/ - m_t} ~ \Big(\frac{1}{k^2 - m_w^2}\Big)^2 ,
\end{align}

I mean (1) has two heavy propagtors in the loop, while (2) has only one heavy propagator, so for the first sight, it seems (2) is the dominant diagram, but this is not the fact .. so anyone can explain why (1) is dominant one ?

 

[Dr.AbeNikIanEdL]

Why do you assume the loop contains top quarks?

 

[Safinaz]

because $\mathcal {M} \propto V_{ib} V_{is}$, so in the best cases the $V_{CKM}$ matrix elements are $V_{tb} V_{ts}$ or $V_{cb} V_{cs}$ . the first choice is the best because $\mathcal {M}$ also proportional to $m_i$

 

[ChrisVer]

aren't you supposed to add them (each individual flavor within the loop)?

 

[Safinaz]

Hi,

If you asking about $Z u_b \bar{u }_c$ vertex, there is $\delta_{bc}$, i.e., Z couples to the same quark flavor.