Discussion Overview
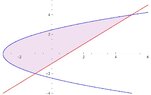
The discussion revolves around evaluating the double integral \( \iint_{R} \, xy \, dA \) over a region \( R \) defined by the line \( y = x - 1 \) and the parabola \( y^2 = 2x + 6 \). Participants explore different approaches to setting up the integral, including the choice of horizontal versus vertical strips.
Discussion Character
- Exploratory, Technical explanation, Debate/contested, Mathematical reasoning
Main Points Raised
- One participant proposes using horizontal strips for integration, defining the bounds as \( \frac{y^2-6}{2} \le x \le y+1 \) and the range for \( y \) as \( -2 \le y \le 4 \).
- Another participant reiterates the previous approach, confirming the bounds and suggesting that the integral can be set up as \( I=\int_{-2}^{4} y\int_{\frac{y^2-6}{2}}^{y+1} x\,dx\,dy \), and claims the result is \( I=36 \).
- A different perspective is introduced, suggesting the use of vertical strips, which would require breaking the integral into two parts, one from -3 to -1 and the other from -1 to 5.
Areas of Agreement / Disagreement
Participants express differing preferences for using horizontal versus vertical strips for integration. There is no consensus on the final setup or solution of the integral, as multiple approaches are presented.
Contextual Notes
Participants mention the need to find intersection points of the curves to determine the limits of integration, but the discussion does not resolve the implications of these choices on the final result.