Double integral to compute capacitance

[chimay]

Hi everyone.

I have quite a basic doubt, and I thought you could help me.
Consider the figure:

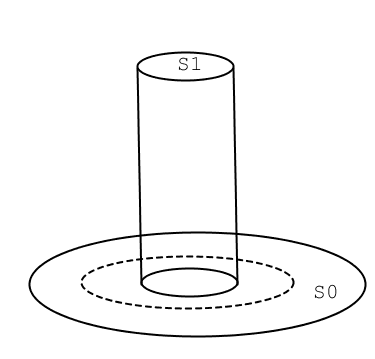
The cylinders S1 is held at a constant potential, and the same applies for the ring identified by S0. All the surroundings are filled with an insulator material. I want to calculate che capacitance between these two metallic "plates".
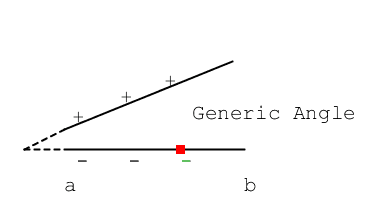
I order to do this, I want to exploit an already known result; it consists of the solution of the following 2-D capacitive coupling (that assumes symmetry along the axis orthogonal to the page):

The approach for the original problem is solving Laplace equation, computing the Electric Field component orthogonal to S0 and deriving superficial charge density. Then integrating all over S0 to compute the total charge.
I have in mind the 3d geometry exhibits cylindrical symmetry, so Laplace equation in cylindrical coordinates is equivalent to the one in polar coordinates solved in one slice, which corresponds to the 2d problem in the second figure.
Can I proceed like this and then integrating along the angle?

Thank you.

 

[Simon Bridge]

I want to exploit an already known result; it consists of the solution of the following 2-D capacitive coupling (that assumes symmetry along the axis orthogonal to the page)...

But is this a good assumption considering you do not have symmetry "along(?) the axis orthogonal to the page".
The picture shows a conducting ring about the base of a cylinder ... if we define axes so z points up the axis of the cylinder, and the x-axis points to the left in the page (so the y-axis is orthogonal to the page) then you can use cylindrical-polar coordinates. ie. you have lots of symmetry about the z axis, not much about the y axis... there's reflection in the x-z plane I suppose...

I don't see how the second figure relates to the first one.
You are thinking to take total charge magnitude Q on both ring and cylinder, determining the potential difference and so the capacitance?

How does this problem come up?

 

[chimay]

You are thinking to take total charge magnitude Q on both ring and cylinder, determining the potential difference and so the capacitance?

Yes, exactly.
I understand your point about the lack of symmetry about the y axis, and actually this is my doubt.
I will try to be more clear.

I should solve the 3D Laplacian equation in cylindrical coordinates.
We recognize that the problem is symmetrical about (*) Φ, the angle present in usual cylindrical coordinates; this means that I can focus on the solution of the problem in one single slice (the plane identified by the red axes):

Now what I am asking is: can I arbitrarily choose to solve the problem in that plane in polar coordinates (r, θ) , can I?

(*) sorry for "along" before, English is not my mother toungue.

 

[Simon Bridge]

I don't think the approach illustrated will be useful - the symmetry you want to exploit does not exist in the setup pictured.

You appear to be defining axes so that the x-y plane is the page, so that the x-axis is horizontal to the right. This points the z-axis out of the page towards the viewer. Your angle $\phi$ is anticlockwaise from the x-axis in the x-y plane. Further, the y-axis is along the side of the cylinder.

If the cylinder has height h and radius a, and the ring has radius b (a<b) then there is charge along the y-axis from 0<y<h (that's $0<r<h$ when $\phi=\frac{\pi}{2}$) and also at x=b-a ($r=b-a$ when $\phi=0$) ... note: the charge density along the y-axis will not be uniform.

How were you planning to go from there to getting the whole field? ie, what about the contribution to the field at x=b-a due to charges 0<y<h at x=-2a?

What is wrong with the cylindrical setup I gave you before?
How does this problem come up?

 

[chimay]

The problem came up in my mind while I was reading some material about how to solve Laplace equation in 2D domains.

I think I got your point, but I want to think about it a little more.
Anyway, I really appreciated your help, thank you a lot.