Double Slit Diffraction with Angled Light

[ab200]

Homework Statement

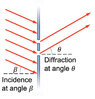
Suppose that a laser beam hits a double-slit apparatus at an angle of β = 40 degrees with respect to the normal. The screen is a distance L away, with slit width a and slit separation d.

Derive a symbolic expression for locating the double-slit interference maxima. At what angle θo is the center of the interference pattern located on the screen? Is the interference pattern symmetric about that angle?

Relevant Equations

dsinθ = mλ (maxima)
tanθ = ym / L

Given that [y][/m] is equal to the position of the interference maxima and is the variable I’m solving for. I got as far as setting up two expressions, one for sinθ and the other for tanθ.

sinθ = (mλ)/d
tanθ = ym/L

My first instinct was to set θ = 40 degrees. By relating sinθ and tanθ to each other through cosθ, I get:

ym = (Lmλ) / (dcos40)

However, I don’t think this makes sense if I have to solve for θo in the second part of the question, so θ must not be fixed. I’m confused about how I am supposed to use the given value of β, but I assume it must be relevant.

If I were able to use small-angle approximation, sinθ ≈ tanθ, but does this still apply here?

 

[hutchphd]

There are many ways to do this. Personally I would look at the two paths and figure the difference in distance using plane geometry. ( Make a good drawing of the path near the plate. ) Then write down the condition for each max assuming β to be held fixed

 

[ab200]

This drawing is from my notes, but this is also what I was thinking for this problem. (Ignore the s1, that’s just a reference point.) I‘m still a bit confused by what you mean with “the condition for each max assuming β to be held fixed.” In this case, β is explicitly held fixed at 40 degrees, no? Is there an assumption I’m making without realizing it?

 

[hutchphd]

Yes I meant that you are interested in solving for θ_m (in fact only for θ₀ ) in terms of the other parameters.

 

[ab200]

I see what you mean and why that is the goal, but I‘m still short-circuiting on what to do in order to get there. For instance, I suppose I could say θm = sin^-1[(mλ)/d] = tan^-1(ym/L), but is that really a sufficient symbolic expression?

And assuming that it is, how does that help me find θo since I don’t know wavelength or slit separation?