Dark85
- 30
- 5
- TL;DR
- If two objects are separated at a distance and start from rest with a uniform acceleration, when will the object behind catch up?
Hey everyone,
I would just like to confirm if the following is correct:
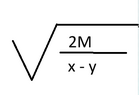
If there are 2 bodies A and B and they both start from rest such that A is "M" meters behind B and once they start, they undergo a uniform acceleration of "x" m/s^2 for A and "y" m/s^2 for B, such that x>y, then A would catch up with B after:

I would just like to confirm if the following is correct:
If there are 2 bodies A and B and they both start from rest such that A is "M" meters behind B and once they start, they undergo a uniform acceleration of "x" m/s^2 for A and "y" m/s^2 for B, such that x>y, then A would catch up with B after: