Draw Nyquist Plot By Hand: Learn How to Determine Stability

[Bypass]

I am trying to understand how to draw nyquist plot.
Lets say the transfer function is

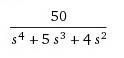
Subbing in jω for s,

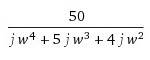***Note: should be (jw)^4 , (jw)^3, (jw)^2

Then separating the Real and Imaginary part,

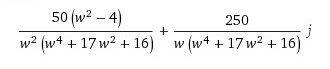
So when
w = 0, in the nyquist plot it is infinity
w = infinity, it is 0
Imaginary intercept is 1.25
For real intercept I am not sure. Since imaginary part is 0 only when w is infinity, i plug in infinity for w in real part. Would the real intercept be infinity or 0? It would be infinity/infinity but numerator is lower order than higher order so would it be 0 instead?

In any case, how am i supposed to plot the rough nyquist plot or at least be able to determine the stability using these 4 points?

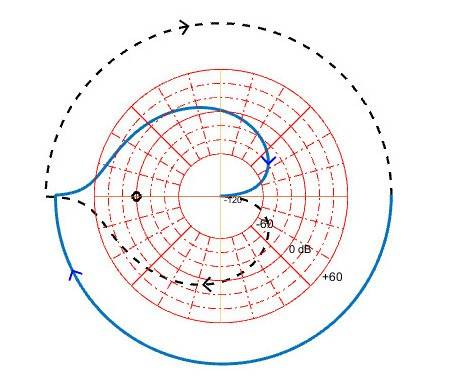
In Matlab the Nyquist plot comes out like this

 

[Hesch]

Sorry, I cannot see what you are doing. You have:

Substituting s with jω, you should get:

50 / ( ( jω )⁴ + 5( jω )³ + 4( jω )² ) =

50 / ( ω⁴ - j5ω³ - 4ω² )

Now, choose a ω and calculate the complex value of the denominator. Do the division and plot the result.

Example: ω=1 → point = ( -4.412 + j7.353 )

 

[Bypass]

Sorry, I cannot see what you are doing. You have:

Substituting s with jω, you should get:

50 / ( ( jω )⁴ + 5( jω )³ + 4( jω )² ) =

50 / ( ω⁴ - j5ω³ - 4ω² )

Now, choose a ω and calculate the complex value of the denominator. Do the division and plot the result.

Example: ω=1 → point = ( -4.412 + j7.353 )

Sorry about that, just a typo. But it is not possible to plug in every single point that encircles the RHP of S-Plane to see how many times the nyquist plot encircles -1 to determine the stability. So my question is what are some key points that I need to plot so I can determine stability of a closed loop system.

 

[Hesch]

Try ω = 1, 2, 3, 4 . . . .

If distances are to small then continue: . . . . 8, 16, 32

If distance is to large between ω=2 and ω=3, then try ω=2.5. It's a "cut and try" process.