- #1
hollowman
- 23
- 6
In digital electronics -- and notably digital reconstruction filters, Shannon and Nyquist theorems -- one encounters "images" (or frequency images).
In digital audio, for example, after the DAC (digital-to-analog converter), one must filter the output of the DAC with an anti-imaging filter (e.g., a low-pass filter).
I've encountered the phenomenon of images in textbook discussions. I'm not clear as to how and why the arise in Nature? I don't think they are like harmonics (which diminish in power (amplitude) the further get from the main freq.)
Simply stated, if I created a single-tone audio pulse (impulse), how and why are its image(s) created?
From wikipedia:
From Ken Pohlmann's Principles of Digital Audio (5th), here are some figures and their captions. I've emboldened all occurrences of term "image":
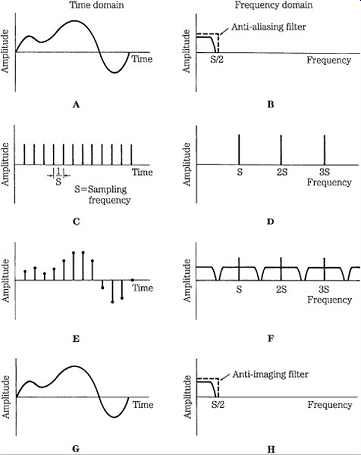
FGR. 2 Time domain (left column) and frequency domain (right column) signals illustrate the process of bandlimited waveform sampling and reconstruction. A. Input signal after anti-aliasing filter. B. Spectrum of input signal. C. Sampling signal. D. Spectrum of the sampling signal. E. Sampled input signal. F. Spectrum of the sampled input signal. G. Output signal after anti-imaging filter. H. Spectrum of the output signal.

FGR. 4 Spectral views of correct sampling and incorrect sampling causing aliasing. A. An input signal bandlimited to the Nyquist frequency. B. Upon reconstruction, images are contained within multiples of the Nyquist frequency. C. An input signal that is not bandlimited to the Nyquist frequency. D. Upon reconstruction, images are not contained within multiples of the Nyquist frequency; this spectral overlap is aliasing; For example, a 29-kHz signal will alias in a 48-kHz sampler.
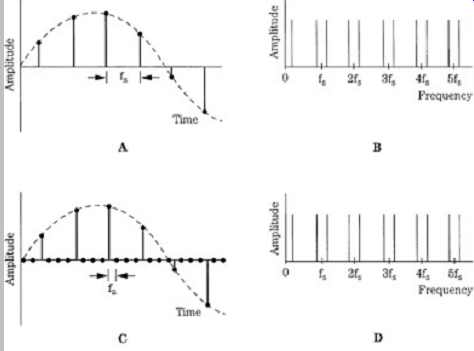
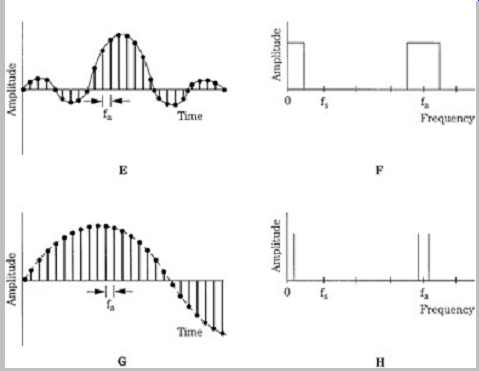
FGR. 12 An oversampling filter resamples and interpolates the signal, using the impulse response; this is shown in the time domain (left column) and frequency domain (right column). A. The input signal is sampled at fs. B. The signal spectrum has images centered around multiples of fs. C. With resampling, zero-valued samples are placed between original samples at some interpolation ratio. D. The spectrum of the oversampled signal is the same as the original signal spectrum. E. The values of a sampled impulse response correspond to the coefficients of the digital filter. F. The transfer function of the filter shows passbands in the audio band and oversampling band. G. The digital filter performs interpolation to form new output sample values. H. The output-filtered signal has images centered around multiples of the oversampling frequency, fa.
In digital audio, for example, after the DAC (digital-to-analog converter), one must filter the output of the DAC with an anti-imaging filter (e.g., a low-pass filter).
I've encountered the phenomenon of images in textbook discussions. I'm not clear as to how and why the arise in Nature? I don't think they are like harmonics (which diminish in power (amplitude) the further get from the main freq.)
Simply stated, if I created a single-tone audio pulse (impulse), how and why are its image(s) created?
From wikipedia:
Sampled data reconstruction filters
The sampling theorem describes why the input of an ADC requires a low-pass analog electronic filter, called the anti-aliasing filter: the sampled input signal must be bandlimited to prevent aliasing (here meaning waves of higher frequency being recorded as a lower frequency).
For the same reason, the output of a DAC requires a low-pass analog filter, called a reconstruction filter - because the output signal must be bandlimited, to prevent imaging (meaning Fourier coefficients being reconstructed as spurious high-frequency 'mirrors'). This is an implementation of the Whittaker–Shannon interpolation formula.
Implementation
While in theory a DAC outputs a series of discrete Dirac impulses, in practice, a real DAC outputs pulses with finite bandwidth and width. Both idealized Dirac pulses, zero-order held steps and other output pulses, if unfiltered, would contain spurious high-frequency content when compared to the original signal. Thus, the reconstruction filter smooths the waveform to remove image frequencies (copies) above the Nyquist limit. In doing so, it reconstructs the continuous time signal (whether originally sampled, or modeled by digital logic) corresponding to the digital time sequence.
From Ken Pohlmann's Principles of Digital Audio (5th), here are some figures and their captions. I've emboldened all occurrences of term "image":
FGR. 2 Time domain (left column) and frequency domain (right column) signals illustrate the process of bandlimited waveform sampling and reconstruction. A. Input signal after anti-aliasing filter. B. Spectrum of input signal. C. Sampling signal. D. Spectrum of the sampling signal. E. Sampled input signal. F. Spectrum of the sampled input signal. G. Output signal after anti-imaging filter. H. Spectrum of the output signal.
FGR. 4 Spectral views of correct sampling and incorrect sampling causing aliasing. A. An input signal bandlimited to the Nyquist frequency. B. Upon reconstruction, images are contained within multiples of the Nyquist frequency. C. An input signal that is not bandlimited to the Nyquist frequency. D. Upon reconstruction, images are not contained within multiples of the Nyquist frequency; this spectral overlap is aliasing; For example, a 29-kHz signal will alias in a 48-kHz sampler.
FGR. 12 An oversampling filter resamples and interpolates the signal, using the impulse response; this is shown in the time domain (left column) and frequency domain (right column). A. The input signal is sampled at fs. B. The signal spectrum has images centered around multiples of fs. C. With resampling, zero-valued samples are placed between original samples at some interpolation ratio. D. The spectrum of the oversampled signal is the same as the original signal spectrum. E. The values of a sampled impulse response correspond to the coefficients of the digital filter. F. The transfer function of the filter shows passbands in the audio band and oversampling band. G. The digital filter performs interpolation to form new output sample values. H. The output-filtered signal has images centered around multiples of the oversampling frequency, fa.