E-Field immediately outside a charged conductor

[llha]

Griffith's says this, and I'm not exactly sure why...

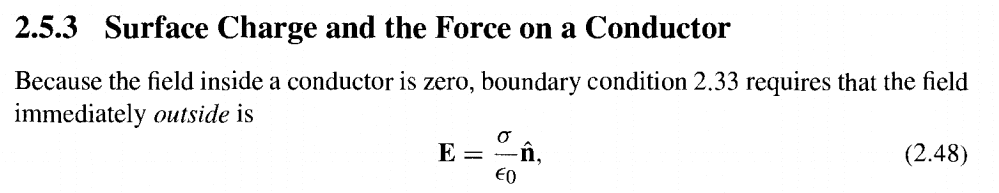
If you had a solid, spherical, and externally induced conductor... Does this mean that IMMEDIATELY outside, when you're infinitesimally close to the surface, E looks like this? If you surround the entire conductor with a Gaussian surface (immediately outside, so not enclosing whatever's inducing the conductor), assuming the conductor is externally induced, wouldn't E = 0 because the net enclosed charge = 0? As you can tell, I'm confused.

 

[marcusl]

The integrated field over a closed surface immediately around the sphere is zero because the field directions cancel. An element of field pointing up at the top,e.g., is canceled by a similar element at bottom pointing down.
EDIT: Sorry, I misread the post. Please disregard what I wrote.

 

[etotheipi]

If you surround the entire conductor with a Gaussian surface (immediately outside, so not enclosing whatever's inducing the conductor), assuming the conductor is externally induced, wouldn't E = 0 because the net enclosed charge = 0? As you can tell, I'm confused.

Is the conductor you're describing uncharged overall? If so, then you can write $\oint_{\Sigma} \mathbf{E} \cdot \mathbf{n} dS = 0$, however note that this does not constrain $\mathbf{E} = \mathbf{0}$ anywhere outside! Where $\sigma < 0$ the field just outside the conductor will point toward the conductor [counted as negative flux through $\Sigma$], and where $\sigma > 0$ the field just outside the conductor will point away from the conductor [counted as positive flux through $\Sigma$]. If the conductor is uncharged, then when integrated over the whole surface, these contributions cancel exactly.

 

[llha]

Is the conductor you're describing uncharged overall? If so, then you can write $\oint_{\Sigma} \mathbf{E} \cdot \mathbf{n} dS = 0$, however note that this does not constrain $\mathbf{E} = \mathbf{0}$ anywhere outside! Where $\sigma < 0$ the field just outside the conductor will point toward the conductor [counted as negative flux through $\Sigma$], and where $\sigma > 0$ the field just outside the conductor will point away from the conductor [counted as positive flux through $\Sigma$]. If the conductor is uncharged, then when integrated over the whole surface, these contributions cancel exactly.

Okay, thank you! I think I understand this better. But I'm still confused why Griffith's says E = δ/ε0n_hat immediately outside a conductor... Wouldn't this only apply for conductors that are infinite planes?

 

[etotheipi]

Okay, thank you! I think I understand this better. But I'm still confused why Griffith's says E = δ/ε0n_hat immediately outside a conductor... Wouldn't this only apply for conductors that are infinite planes?

It's a general result, that at any discontinuity with surface charge density $\sigma$, the normal component of the field undergoes a change of $\sigma / \varepsilon_0$. Consider a tiny Gaussian pillbox that cuts through the surface, and suppose that the normal components of the fields on either side are $E_1 \mathbf{z}$ and $E_2 \mathbf{z}$, where $\mathbf{z}$ is a unit vector normal to the surface [we can, here, ignore the tangential components (which are continuous), because they will not contribute to flux]. You have$$\int_{\Sigma} \mathbf{E} \cdot d\mathbf{S} = E_2 A - E_1 A = \frac{\sigma A}{\varepsilon_0} \implies E_2 = E_1 + \frac{\sigma}{\varepsilon_0}$$You can see that the normal component of the field has incremented by an amount $\sigma / \varepsilon_0$.

At the surface of a conductor (of any shape!), the field inside is zero, so just outside some point on the conductor the field is going to have normal component $\sigma / \varepsilon_0$.

With your example of an infinite, thin charged plane, say occupying the y-z plane, then the field on one side is $- (\sigma/ 2 \varepsilon_0) \mathbf{x}$, whilst the field on the other side is $(\sigma/ 2 \varepsilon_0) \mathbf{x}$. Notice that, again, the increment in the field is $(\sigma/ 2 \varepsilon_0) \mathbf{x} - (- \sigma/ 2 \varepsilon_0) \mathbf{x} = (\sigma / \varepsilon_0) \mathbf{x}$.

 

[kuruman]

Wouldn't this only apply for conductors that are infinite planes?

When is a plane infinite? In this case, as in many other similar situations when you are doing physics, one should not imagine a mathematical infinity. Here "infinite" means "very large". Of course "very large" is meaningless unless you have a scaling distance to compare against. The idea behind the boundary condition is that it holds for any finite conductor if you are at a scaling distance $\delta$ above its surface that is very small relative to the local radius of curvature, $R$. In the limit $\delta\rightarrow 0$ ($\delta <<R$), you are arbitrarily close to the surface which looks like an "infinite plane" much like the Earth looks flat when you are a meter or so above its surface.