Wmdajt
- 3
- 0
- Homework Statement
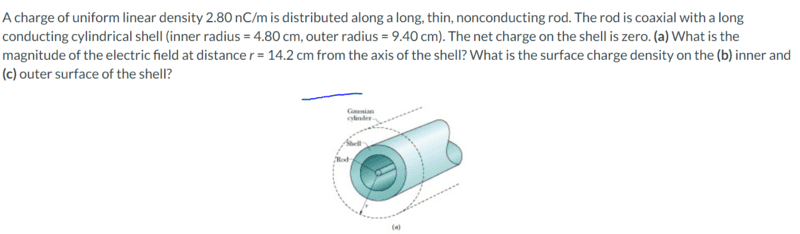
- A charge of uniform linear density 2.8nC/m is distributed along a long, thin, nonconducting rod. The rod is coaxial with a long conducting cylindrical shell (inner radius =4.8 cm, outer radius =9.40 cm). The net charge on the shell is zero. (a) What is the magnitude of the electric field 14.2 cm from the axis of the shell? What is the surface charge density on the (b) inner and (c) the outer surface of the shell?
- Relevant Equations
- E=λ/(2πε0r)
ε0ϕ = q
In this question I need to find the inner and outer charge density of the shell I did part A just fine, I used the formula for an electric field due to a line charge, but parts B and C is what's really confusing me. I'm not really sure how to go about it, I placed a spherical gaussian surface inside of the shell which gives me a flux of E*π*r^2. I didn't have a reason to attempt this, I was just seeing where it would take me. Any help would be appreciated, thanks!