Easy center of mass/toppling question?

[Nanosuit]

[Mentor's note: this was originally posted in a non-homework forum and then moved here, so it doesn't use the standard homework forums template.]

I am studying the edexcel A level M2 mathematics module and came across this question that i don't know how to do.Even the book doesn't have any material to help me out with this sort of questions.
Sorry If I've posted this in the wrong section.Since it said 'classical physics' so i thought it should go here :P

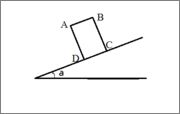
A thin uniform rectangular metal plate ABCD of mass M rests on a rough plane inclined at an angle σ to the horizontal.the plate lies in a vertical plane containing a line of greatest slope of the plane, with the edge CD in contact with the plane and C further up the plane than D, as shown in the figure.The lengths of AB and BC are 10cm and 30cm respectively.The plane is sufficiently rough to prevent the plate from slipping.

a)Find, to the nearest degree, the greatest value which σ can have if the plate does not topple.

A small stud of mass m is fixed to the plate at the point C

b)Given that tanσ=1/2, find, in terms of M, the smallest value of m which will enable the plate to stay in equilibrium without toppling.

I could do a) but got stuck at b).I tried applying principle of moments for m but all to no avail.

Answers- a) 18' b) 0.25M

Thanks in advance :)

 

[tiny-tim]

Hi Nanosuit! Welcome to PF!

(btw, please use the homework section next time: see https://www.physicsforums.com/forumdisplay.php?f=152)

I could do a) but got stuck at b).I tried applying principle of moments for m but all to no avail.

Show us your moments equation for b).

 

[Nanosuit]

I didn't know what else to do.I have no idea how to do that :/

 

[tiny-tim]

Hi Nanosuit!

There are three forces on the plate-and-stud:

the weight of the plate
the weight of the stud
the reaction force from the slope​

the two weights obviously act vertically downward

the line of action of the weight of the plate goes through the centre of mass of the plate

the plate will start to topple when the reaction force goes through the bottom edge, D

so take moments about D (because that will easily tell you when the reaction force goes through D) …

show us what you get ​

 

[Nanosuit]

Hi Nanosuit!

There are three forces on the plate-and-stud:

the weight of the plate
the weight of the stud
the reaction force from the slope​

the two weights obviously act vertically downward

the line of action of the weight of the plate goes through the centre of mass of the plate

the plate will start to topple when the reaction force goes through the bottom edge, D

so take moments about D (because that will easily tell you when the reaction force goes through D) …

show us what you get ​

thanks :)
Should i consider only x-coordinates(taking DC as the x-axis) or y as well?

 

[tiny-tim]

Should i consider only x-coordinates(taking DC as the x-axis) or y as well?

I don't understand the relevance of your question

Draw the forces on the diagram, then calculate the moments about D.

 

[Nanosuit]

It would be better if you could tell me the rules? Because i need help immediately.This types of math are completely foreign to me since even the books don't say how we should approach such problems

Sorry if i sound impatient

I tried outlining the forces and resolving them.I did what i could:

 

[tiny-tim]

Hi Nanosuit!

(it would help if you'd put the centre of mass in the centre, and if you avoided making the Mg weight go through D)

The reaction force is not in the normal direction (since it includes the friction force).

It is obviously vertical (why?).

(And the stud does not have its own reaction force, you need to draw the reaction force for the whole plate-plus-stud.)

As I said before, the plate-plus-stud will start to topple when the reaction force goes through the bottom edge, D.