Efficient Solutions for the Poisson-Boltzmann Equation in a Rectangular Domain

[Assaf Peled]

Hello,

I'm trying to find either an analytical or a semi-analytical method for solving the following P-B Eq.

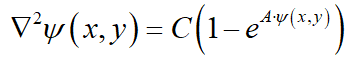
with C and A being two constants. The equation is to be solved within a rectangle with constant boundary conditions.

If anyone has a clue, I'll be grateful.

Have a good evening.

 

[NFuller]

Have you tried using a Fourier transform? The exponential in your equation makes that method seem promising.

 

[Assaf Peled]

Not sure that you're right because the exponential term contains the function itself rather than the independent variables x or y.

 

[NFuller]

In that case, the only other method I know would be to write the right hand side as a power series centered at the origin of the domain and truncate the series to some low order, like first or second, and solve the resulting PDE.