- #1
ujo142
- 4
- 0
- Homework Statement
- Solving heat equation with internal heat cources
- Relevant Equations
- u_{t} = u_{xx} + q(x)/P,
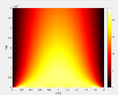
Hi, I am solving heat equation with internal heat sources both numerically and analytically. My graphs are nearly identical but! analytical one have problem at the beginning and at the end for my domain. Many people have used the same technique to solve it analytically and they got good answers. Example solution from my professor had the same issue. I cannot ask him at this time, university is closed in this week. Does anyone have at least idea what is causing this problem and how to solve it? I came up with an idea that i have some kind of tradeoff between initial and boundary conditions.
Problem: u_{t} = u_{xx} + q(x)/P, q(x) = (-x^2+2x), P=const, x: [0,L], t: [0, 40000]
u(0,t) = u(L,t) = 0 u(x, 0) = T0 = 20U can see that analytical solution does not have 20*C close to edges with small time.
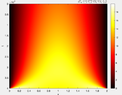
Problem: u_{t} = u_{xx} + q(x)/P, q(x) = (-x^2+2x), P=const, x: [0,L], t: [0, 40000]
u(0,t) = u(L,t) = 0 u(x, 0) = T0 = 20U can see that analytical solution does not have 20*C close to edges with small time.