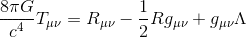Discussion Overview
The discussion revolves around the use of index notation in Einstein's field equations, particularly focusing on the role of the metric tensor and the summation convention in tensor notation. Participants explore how these concepts relate to the structure of the equations and the implications for understanding tensor components.
Discussion Character
- Technical explanation, Conceptual clarification, Debate/contested
Main Points Raised
- Some participants note that the metric tensor employs Einstein summation notation, while questioning how this applies to the field equations, which they describe as having a tensor form.
- One participant clarifies that a tensor itself does not utilize the summation convention, which is specifically for simplifying the contraction of indices, and points out that the indices in the Einstein field equations are free indices without contraction.
- Another participant expresses confusion about whether the components of the equations are obscured by the notation.
- It is mentioned that the Ricci tensor and Ricci scalar involve contractions of the Riemann curvature tensor, suggesting that while there are implicit contractions, they are already accounted for in the equations.
- A participant references a geometric interpretation of the metric tensor involving a triangle in curved space, indicating a conceptual approach to understanding the tensor's application.
Areas of Agreement / Disagreement
Participants exhibit some agreement on the nature of the summation convention and its application, but there remains disagreement and uncertainty regarding the visibility of contractions and the interpretation of the metric tensor in the context of the field equations.
Contextual Notes
Limitations include potential misunderstandings about the visibility of tensor components and the specific application of the summation convention in the context of the Einstein field equations.