Elastic energy and force on an object

[Joshb60796]

Homework Statement

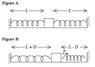
Two identical ideal massless springs have unstretched lengths of 0.25m and spring constants of 700N/m. The springs are attached to a small cube and stretched to a length L of 0.30m. One spring on the left and one on the right. An external force P pulls the cube a distance of D = 0.020m to the right and holds it there. Find the external force P, that holds the cube in place. A picture has been attached for reference.

Homework Equations

Work done on a spring = (1/2)kx₂²-(1/2)kx₁²
Work done by a spring = (1/2)kx₁²-(1/2)kx₂²

The Attempt at a Solution

I tried to compute the amount of work done by each spring and then take that work and divide by double the distance because there are two springs, to figure out the force but I came up with numbers less than one and the answer is supposed to be 28N. I'm not sure if the fact that both springs are already in tension when they were stretched from .25m to .30m and I have to figure in potential energy. It seems that one of the springs, as the block is moved, passes through it's zero force point where as the opposite spring is just stretched further. This passing through the zero point confuses me too. Thank you for any help you can provide.

 

[Drmarshall]

Not double the distance

Work 1 = force 1 times distance 1
Work 2 = force 2 times distance 2

 

[Joshb60796]

How do I find the distance? The springs are relaxed at .25 but in the problem they start out stretched to .30. Do I consider .30 as the new zero or does the fact that they are pre-stretched add more complexity. Do I consider .25 as zero and add the .5 to it in figuring out the distance? I know that force multiplied by displacement gives work but I know neither force nor work. I understand that whatever work is done to one side may be provided by the other side because I'm compressing one spring and stretching the other but one spring will be decompressing till it reaches the original .25 stretch and then it will be compressing.

 

[Doc Al]

Forget about work. You are told that the mass is in equilibrium at the new position. Figure out what force each spring exerts on the mass in that position. Then you can figure out what the force P must be to hold the mass in place.

 

[Joshb60796]

hmmm ok, so for every meter the springs are compressed or stretched, it requires 700N of force. The spring on the left side would be 0.25m unless a force was present. The problem states it is at 0.30m so currently there is (0.05m*700N/m) 35N of force stored as potential energy in the spring. As I progress to the second state of the problem in which the object is moved to the right, am I adding to this 35N of force or starting from 0?

 

[Doc Al]

hmmm ok, so for every meter the springs are compressed or stretched, it requires 700N of force. The spring on the left side would be 0.25m unless a force was present. The problem states it is at 0.30m so currently there is (0.05m*700N/m) 35N of force stored as potential energy in the spring.

Each spring exerts a force of 35 N on the mass, giving a net force of 0. Forget about potential energy--this is a statics problem.

As I progress to the second state of the problem in which the object is moved to the right, am I adding to this 35N of force or starting from 0?

I suggest finding the actual force exerted by each spring, which means you use the total stretch of the spring from its unstretched length. (But if I understand what you mean, it won't matter to the answer you get.)

 

[Joshb60796]

Ok so I should maybe look at one spring's force and figure that out, then just double the force because I have two springs? Since force = mass * acceleration and I'm holding the object to the right with no movement, don't I have zero acceleration and therefore no net force which means that potential energy is responsible for balancing the force that I'm applying with P force? Potential energy is half of the spring constant multiplied by the square of the displacement but I'm left with Joules and am going back into a work problem to get the force which you are saying is the wrong direction to follow. I'm confused.

 

[Doc Al]

Ok so I should maybe look at one spring's force and figure that out, then just double the force because I have two springs?

No. Once the mass is displaced, the springs will have different amounts of stretch and thus will exert different forces.

Since force = mass * acceleration and I'm holding the object to the right with no movement, don't I have zero acceleration and therefore no net force which means that potential energy is responsible for balancing the force that I'm applying with P force?

Again, forget about potential energy! Newton's 2nd law says that ƩF = ma, which you'll use to find P. First find the forces exerted by the springs.

 

[Joshb60796]

Ok, so F=mass*acceleration. the mass is not mentioned so I'll call it m, and since it's holding the object with no movement that means that there is no acceleration so I have force equals m times zero so there is zero force?

 

[Doc Al]

Ok, so F=mass*acceleration. the mass is not mentioned so I'll call it m, and since it's holding the object with no movement that means that there is no acceleration so I have force equals m times zero so there is zero force?

There is zero net force. The mass is in equilibrium. The force P must be equal and opposite to the force exerted by the springs to make the net force equal to zero. So find the force that the springs exert on the mass.

 

[Joshb60796]

I'm assuming I use the spring constant of 700N/m in conjunction with the displacement which for one spring is [(0.30m-0.25m)+0.020m]=0.07m then multiply by 700 so 49N for that side and [(0.30-0.25)-0.020]=0.03m then multiply by 700 so 21N for that side but in the opposite direction so -21N for a total of 28N right?

 

[Doc Al]

I'm assuming I use the spring constant of 700N/m in conjunction with the displacement which for one spring is [(0.30m-0.25m)+0.020m]=0.07m then multiply by 700 so 49N for that side and [(0.30-0.25)-0.020]=0.03m then multiply by 700 so 21N for that side but in the opposite direction so -21N for a total of 28N right?

Exactly! The total force exerted by the springs is 28 N to the left. So what must P be to produce equilibrium at that point?

 

[Joshb60796]

It must also be 28N but to the right. So this whole problem's main complexity was just figuring out the distance that the springs were stretched and then multiplying by the spring constant?

 

[Doc Al]

It must also be 28N but to the right. So this whole problem's main complexity was just figuring out the distance that the springs were stretched and then multiplying by the spring constant?

Yep. Nothing to do with potential energy or work. Just Hooke's law.

 

[Joshb60796]

hmm I assumed it would be harder and more complex. Thank you sir for all your help and patience.