waltonhcky05
- 2
- 0
I'm given a stress strain diagram for a sample of steel that has an original diameter of 0.5in and a gauge length of 2in. The sample is loaded to 70ksi and the question asks for the amount of elastic recovery and permanent elongation of the sample. The actual graph is shown below...
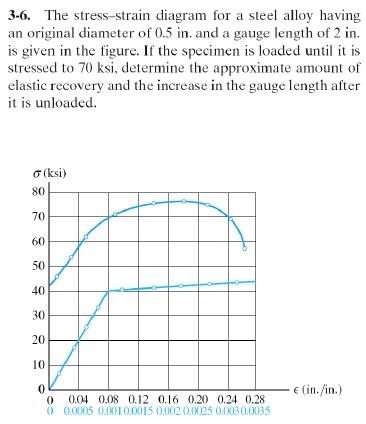
I know that I would need to draw a line that is of the same slope as modulus of elasticity to find the elastic recovery and permanent set. Where the permanent set is just the x intercept of that new line, but what's confusing me is the two lines shown on the graph and which one I should be using to draw this new line. Also, once I find out which line I should be using, from what point on the curve should I actually draw the new line from?
Thanks for any help!
I know that I would need to draw a line that is of the same slope as modulus of elasticity to find the elastic recovery and permanent set. Where the permanent set is just the x intercept of that new line, but what's confusing me is the two lines shown on the graph and which one I should be using to draw this new line. Also, once I find out which line I should be using, from what point on the curve should I actually draw the new line from?
Thanks for any help!
Last edited: