Converting Voltage into Pressure

[guyvsdcsniper]

Homework Statement

Convert Voltage into pressure

Relevant Equations

y=mx+b

I am measuring the index of refraction of air using a Michelson interferometer.

This set up includes a gas chamber that is placed on of the paths of source laser after it passes through a beam splitter. The gas chamber is pumped to vacuum, and then air is allowed to slowly enter the gas chamber. The introduction of air is enough to slow down the laser passing through it to cause a phase shift. The two beams of the laser then recombine at the beam splitter and emit a sweeping interference pattern onto a photodetector, that measures the the change in interference pattern as voltage difference.

The change in pressure in the gas chamber is measured via voltage difference via a pressure gauge. Vacuum is approximately -9.409 V and atmosphere is approximately .010V.

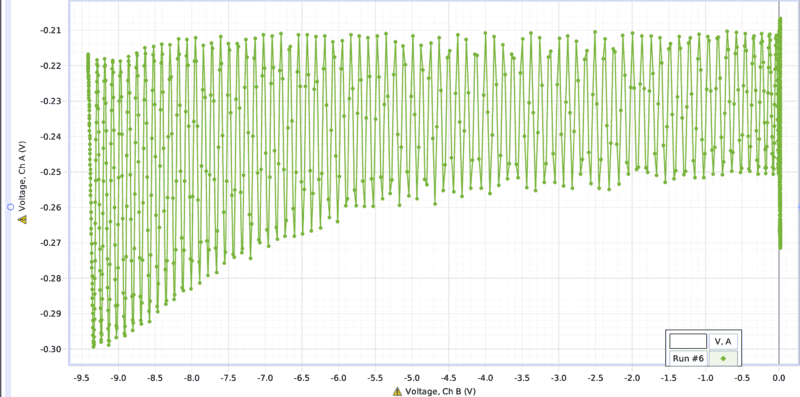
My goal is to take the data from one of these runs and plot it as Intensity of the photo detector (Ch A) vs the pressure of the pressure gauge(Ch B.).

I am fine with leaving the intensity in terms of voltage, but leaving my x axis as pressure in terms of voltage doesnt seem right to me.

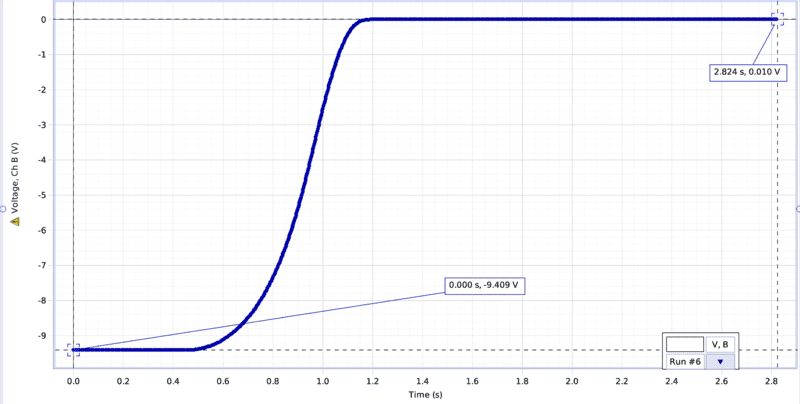
So I plotted the pressure gauge voltage with respect to time, which can be seen in the photo below, plotted in blue. I found the slope to be 3.34 and my y intercept be -9.409. So I have the equation y = 3.34x-9.409, where x is a certain time in the run. This should give me the voltage at any instance of time. I tried plugging in certain time values but the voltage values I receive dont match whats actually on the graph.

If this above equation did work, I thought that if 1atm = 9.409 Volts, I can take the ratio of 1atm/y and convert volts to atm.

But this doesn't seem to work for me.

 

[.Scott]

Your pressure voltage does not change linearly as pressure changes. So you can't simply use a ratio.
One intermediate goal would be to plot intensity as a function of pressure - but you don't seem to have collected the right kind of information to do that kind of calibration.

I would try to set up some situation where I knew the pressure vs. time function and use that to determine the pressure vs. $V_b$ function.

 

[guyvsdcsniper]

Your pressure voltage does not change linearly as pressure changes. So you can't simply use a ratio.
One intermediate goal would be to plot intensity as a function of pressure - but you don't seem to have collected the right kind of information to do that kind of calibration.

I would try to set up some situation where I knew the pressure vs. time function and use that to determine the pressure vs. $V_b$ function.

So maybe I can try to find a curve fit for the $V_b$ vs time graph?

 

[kuruman]

If I understand you correctly, you want to convert voltage readings into pressure readings. To do that, first you evacuated your chamber and recorded -9.409 V. Then you let air in which filled your chamber to atmospheric pressure in about 1.2 seconds judging from your graph. That's pretty fast. Collecting data on the fly in a couple of seconds may be fast but has its disadvantages. Pressure is meaningful if it is the same everywhere in the chamber at any given time.

In any case, why do you care to calibrate the abscissa in pressure units? If I understand the experiment correctly, all you need in order to find the index of refraction of air is the number of fringes that go by from vacuum to atmospheric pressure. You can get these from the first plot in green. Note that the green sinusoidal fluctuations are closer together near the two ends than in the middle. This means that the fringes don't move at constant speed as the chamber is filled with air which probably means the air is not rushing in at a uniform rate

That said, doesn't the manual of the instrument that you have used have a calibration formula that tells you how to convert voltage to pressure units?

 

[DaveE]

Check for manufacturers data for your pressure sensor. They should have characterized this. If the curve is non-linear, it's probably pretty well behaved and could be calibrated with just a few known data points.

 

[DaveE]

Slowly introducing air into the chamber probably does not equate to a constant change in pressure, since the pressure drop across the valve isn't constant.

 

[Steve4Physics]

I am fine with leaving the intensity in terms of voltage, but leaving my x axis as pressure in terms of voltage doesnt seem right to me.

The manufacturer of the pressure transducer should provide calibration data (e.g. a pressure-voltage graph). Ask the technician in charge if this is available – usually this sort of information is kept on file.

So I plotted the pressure gauge voltage with respect to time, which can be seen in the photo below, plotted in blue. I found the slope to be 3.34 and my y intercept be -9.409. So I have the equation y = 3.34x-9.409, where x is a certain time in the run. This should give me the voltage at any instance of time. I tried plugging in certain time values but the voltage values I receive dont match whats actually on the graph.
I don't understand what you have done. If you have assumed that pressure increases linearly with time, that is unlikely unless the system has been design to do that.

Edited.

 

[guyvsdcsniper]

If I understand you correctly, you want to convert voltage readings into pressure readings. To do that, first you evacuated your chamber and recorded -9.409 V. Then you let air in which filled your chamber to atmospheric pressure in about 1.2 seconds judging from your graph. That's pretty fast. Collecting data on the fly in a couple of seconds may be fast but has its disadvantages. Pressure is meaningful if it is the same everywhere in the chamber at any given time.

In any case, why do you care to calibrate the abscissa in pressure units? If I understand the experiment correctly, all you need in order to find the index of refraction of air is the number of fringes that go by from vacuum to atmospheric pressure. You can get these from the first plot in green. Note that the green sinusoidal fluctuations are closer together near the two ends than in the middle. This means that the fringes don't move at constant speed as the chamber is filled with air which probably means the air is not rushing in at a uniform rate

That said, doesn't the manual of the instrument that you have used have a calibration formula that tells you how to convert voltage to pressure units?

You are correct, all I need is the number of fringes. I have only been attempting to calibrate the abscissa in pressure units because when presenting my graph, I thought it would seem more presentable by converting the readings of the pressure gauge to the Si unit of pressure.

The pressure gauge just states on the back of it that 1atm is plus/minus 10V.

My lab manual only states the following regarding the pressure gauge :

 

[guyvsdcsniper]

The manufacturer of the pressure transducer should provide calibration data (e.g. a pressure-voltage graph). Ask the technician in charge if this is available – usually this sort of information is kept on file.

So I plotted the pressure gauge voltage with respect to time, which can be seen in the photo below, plotted in blue. I found the slope to be 3.34 and my y intercept be -9.409. So I have the equation y = 3.34x-9.409, where x is a certain time in the run. This should give me the voltage at any instance of time. I tried plugging in certain time values but the voltage values I receive dont match whats actually on the graph.
I don't understand what you have done. If you have assumed that pressure increases linearly with time, that is unlikely unless the system has been design to do that.

Edited.

Yes I assumed it was linear but now looking back it does not make sense, as the voltage vs time graph is obviously not linear

 

[.Scott]

The manufacturer of the pressure transducer should provide calibration data (e.g. a pressure-voltage graph). Ask the technician in charge if this is available – usually this sort of information is kept on file.

I have an alternative guess. Given that we are receiving a voltage value that appears to be very non-linear, my guess is that we are wired up to little more than a piezo crystal, a resistor bridge, and an op amp. If that is the case, you actually need that piezo circuit output and a temperature reading in order to get good calibration of both the pressure and temperature - and the calibration parameters (coefficients) will be different for each pressure/temperature device pair.

So to @guyvsdcsniper : Sure, if this is already a calibrated device, then collect and use whatever you can get form the manufacturer - but I won't be holding my breath.

 

[.Scott]

So maybe I can try to find a curve fit for the $V_b$ vs time graph?

Yes. Fit a curve - with or without a function.
You could also go linear - but if you do, stick to the $V_b$ measurements between -7 and -1 volts, since those are roughly linear.

 

[guyvsdcsniper]

Yes. Fit a curve - with or without a function.
You could also go linear - but if you do, stick to the $V_b$ measurements between -7 and -1 volts, since those are roughly linear.

Using matlab, I can use interpolant curve fitting, which fits precisely but does not give me a function. But without the function, how will I be able to translate the $V_b$ to pressure?

 

[kuruman]

You are correct, all I need is the number of fringes.

So count them. In the green plot you have the intensity rising and falling. How do you interpret this if not maxima and minima going by? Just count peaks (or valleys).

 

[guyvsdcsniper]

So count them. In the green plot you have the intensity rising and falling. How do you interpret this if not maxima and minima going by? Just count peaks.

Well yeah I counted the peaks and I got a pretty close index of refraction. I dont have a problem with this part, my only problem is trying to convert the voltage of the pressure sensor, $V_b$, into an actual unit of pressure.

Edit: and I only want to do that to make my data more presentable

 

[DaveE]

Using matlab, I can use interpolant curve fitting, which fits precisely but does not give me a function. But without the function, how will I be able to translate the $V_b$ to pressure?

I have often looked at my data and first chosen a function, then essentially fit it by trial and error. It sounds tedious, but very often you can get a good, albeit non-optimal, fit pretty quickly. Of course you have to choose an appropriate function. This works really well if you have a physical basis for your function choice.

Some SW tools will do this, my ancient copy of Excel, for example. Then it will give you the function's constants for best fit. Excel only has a few functions available, however.

A polynomial fit, like a Taylor's series, can be done to arbitrary precision, but it can appear clumsy for some data where another simple function (1/x, sqrt(x), exp(x), etc.) is more appropriate.

 

[guyvsdcsniper]

I have often looked at my data and first chosen a function, then essentially fit it by trial and error. It sounds tedious, but very often you can get a good, albeit non-optimal, fit pretty quickly. Of course you have to choose an appropriate function. This works really well if you have a physical basis for your function choice.

Some SW tools will do this, my ancient copy of Excel, for example. Then it will give you the function's constants for best fit. Excel only has a few functions available, however.

A polynomial fit, like a Taylor's series, can be done to arbitrary precision, but it can appear clumsy for some data where another simple function (1/x, sqrt(x), exp(x), etc.) is more appropriate.

I tried a 9th order polynomial fit but it still didnt look that good. The best fit I could get was a fourier curve fit, which makes sense given the shape of the graph. But I am not really sure if thats the best option as its a very messy equation with cosines and sines.

 

[.Scott]

I tried a 9th order polynomial fit but it still didnt look that good. The best fit I could get was a fourier curve fit, which makes sense given the shape of the graph. But I am not really sure if thats the best option as its a very messy equation with cosines and sines.

Make things easy on yourself - stick width -7 to -1 V.

 

[guyvsdcsniper]

Make things easy on yourself - stick width -7 to -1 V.

I am thinking this is the way to go after messing with curve fitting all day.

But sticking with -7 to -1 V, that would mean I have to exclude all data points outside that range?

 

[DaveE]

I am thinking this is the way to go after messing with curve fitting all day.

But sticking with -7 to -1 V, that would mean I have to exclude all data points outside that range?

yes, but why do you need them anyway?

 

[kuruman]

Edit: and I only want to do that to make my data more presentable

I understand. Are you also thinking of converting the vertical axis to intensity units? The usefulness of having one axis in appropriate units and the other in arbitrary units is limited. Besides, having both axes in Volts is an honest presentation of exactly what you measured without any massaging.

 

[guyvsdcsniper]

I understand. Are you also thinking of converting the vertical axis to intensity units? The usefulness of having one axis in appropriate units and the other in arbitrary units is limited. Besides, having both axes in Volts is an honest presentation of exactly what you measured without any massaging.

I have a inclination to just leave both axis in terms of Volts, but I did just come across this in my lab manual:

Do you think it would still be appropriate to leave it in volts in this context?

 

[kuruman]

Why is the lab manual concerned with the slope of the index of refraction vs. pressure graph? More importantly, why have you taken all these measurements? What is the object of your experiment?

Also, I question the necessity of having to worry about $P_i$. If you used a decent mechanical pump to evacuate your chamber, you can safely assume that $P_i \approx 0$ because, in all likelihood, the mean free path of the air molecules is greater than the size of your chamber.

 

[guyvsdcsniper]

Why is the lab manual concerned with the slope of the index of refraction vs. pressure graph? More importantly, why have you taken all these measurements? What is the object of your experiment?

Also, I question the necessity of having to worry about $P_i$. If you used a decent mechanical pump to evacuate your chamber, you can safely assume that $P_i \approx 0$ because, in all likelihood, the mean free path of the air molecules is greater than the size of your chamber.

I am not sure, the lab manual does state anything other than plotting the two.
I have searched online for other lab reports and I dont see any rely on this graph. Given the last equation from the lab manual screen shot I posted, I can simply cancel the common factor of the change in pressure and create a function $n = 1 +\frac{\Delta m \lambda_0}{2d}$. From this I can just plot the number of peaks vs the index of refraction.

Does this function seem reasonable? I've seen other lab reports and they graphed number of counts vs pressure but I dont see why the function above isnt just as useful.

 

[kuruman]

From this I can just plot the number of peaks vs the index of refraction.

I think you got it backwards. You want to plot the index of refraction on the vertical axis vs. the number of fringes on the horizontal axis. You can then fit a straight line and see how close the slope comes to $\frac{\lambda_0}{2d}$ and the intercept to 1 which I assume you know or can measure. The latter number should give you an idea of how good a vacuum you pulled on the chamber.

 

[guyvsdcsniper]

I think you got it backwards. You want to plot the index of refraction on the vertical axis vs. the number of fringes on the horizontal axis. You can then fit a straight line and see how close the slope comes to $\frac{\lambda_0}{2d}$ and the intercept to 1 which I assume you know or can measure. The latter number should give you an idea of how good a vacuum you pulled on the chamber.

Sorry I meant to write index vs fringes, that is what I ended up doing.