Electric field at a point (charged ring)

[grantrudd]

this is the second part of a 3 part question the first part was:

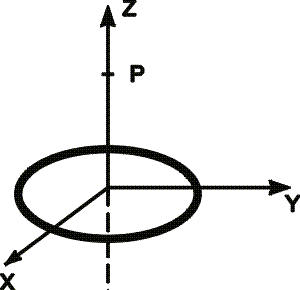
A uniform circular ring of charge Q=4.40 microCoulombs and radius R=1.30cm is located in the x-y plane, centered on the origin as shown in the figure. What is the magnitude of the electric field E at point P, located at z=3.30 cm?

i used E=F/q and integrated to get the formula

E=KQz/(z^2+a^2)^3/2 and got an answer of 2.92x10^7 N/C, which was right

now onto my question

Homework Statement

Consider other locations along the positive z-axis. At what value of z does E have its maximum value?

Homework Equations

i figure the equation i figured out in part 1 of this question would be relevant

E=KQz/(z^2+a^2)^3/2

The Attempt at a Solution

i decided to take the derivative with respect to z of the equation above, and i believe that might be where i am making a mistake. to save the hassle of writing out the long work, here is what i got.

dE/dz= -1.5KQz(z^2+a^2)^1/2

the only critical point i am getting from this derivative is z=0, which makes sense because the electric field is at a minimum at that point. I am thinking that as z approaches infinity, the cosine between the individual vectors and the resultant vector approaches 1, which would lead to a maximum. can anyone tell where i went wrong or if my logic is off?

thanks
Grant

 

[Doc Al]

i decided to take the derivative with respect to z of the equation above, and i believe that might be where i am making a mistake. to save the hassle of writing out the long work, here is what i got.

dE/dz= -1.5KQz(z^2+a^2)^1/2

Redo that derivative.

 

[flatmaster]

you're thinking is generally on track. Re-check the derivative. Don't forget you have two z's. You need to use either the quotient rule or product rule. Personally, I don't even remember the quotient rule. I always turn it into a product.

E=KQz/(z^2+a^2)^3/2 = KQz(z^2+a^2)^-3/2

Notice, Rather than dividing, it is now a product with a negative exponent. This form is useful because it allows everything to be in a line multiplying rather than messing around with division signs.

 

[grantrudd]

this derivative is really fouling me up here. this time, i used the product rule, and i got

-9/2zKQ(z^2+a^2)^-5/2+KQ(z^2+a^2)^-3/2

then i factored out a KQ(z^2+a^2)^-3/2 to get

KQ(z^2+a^2)^-3/2(-9/2z((z^2+a^2)^-1)+1)

after that, i broke it apart into factors and set each factor equal to zero:

KQ(z^2+a^2)^-3/2 is zero as z approaches infinity

with the other factor, i figured out that the critical points to be approximately -1 and 3.75x10^-5, neither of which are right, or seem right in my mind. did i make another mistake in the derivative?

 

[flatmaster]

I think you're good so far. One thing you could try...

Remember you're going to be setting this derivative equal to zero in the end, so any constants that multiply EVERYTHING divide out. For example, the constants KQ divide out.

Your final answer is going to be a "plus or minus" answer. If you look at the symetry of the problem, the same distance in the -z direction behaves exactly the same way.

Like you said, you have two expressions multiplying that are equal to zero. One of them must be zero. What if you say

(z^2+a^2)^-3/2=0?