- #1
zgs
- 3
- 0
1.
I think this should an easy one:
Homework Statement
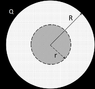
Consider an insulating sphere of radius R centered on the origin with total charge Q uniformly distributed throughout the volume of the sphere. What is the electric field E inside the sphere at a distance r from the origin? (i.e. r<R)
They list Vshpere=4/3 ∏r^3 and Asphere=4∏r^2
I know E=kQ/r^2=f/q
Multiple choice and I thought it was just E=kQ/r^2. Answer is really E=kQr/R3. Where did R^3 come from? I have to be missing an equation from my notes.. I must have to somehow incorporate the volume.
I think this should an easy one:
Homework Statement
Consider an insulating sphere of radius R centered on the origin with total charge Q uniformly distributed throughout the volume of the sphere. What is the electric field E inside the sphere at a distance r from the origin? (i.e. r<R)
Homework Equations
They list Vshpere=4/3 ∏r^3 and Asphere=4∏r^2
I know E=kQ/r^2=f/q
The Attempt at a Solution
Multiple choice and I thought it was just E=kQ/r^2. Answer is really E=kQr/R3. Where did R^3 come from? I have to be missing an equation from my notes.. I must have to somehow incorporate the volume.