SUMMARY
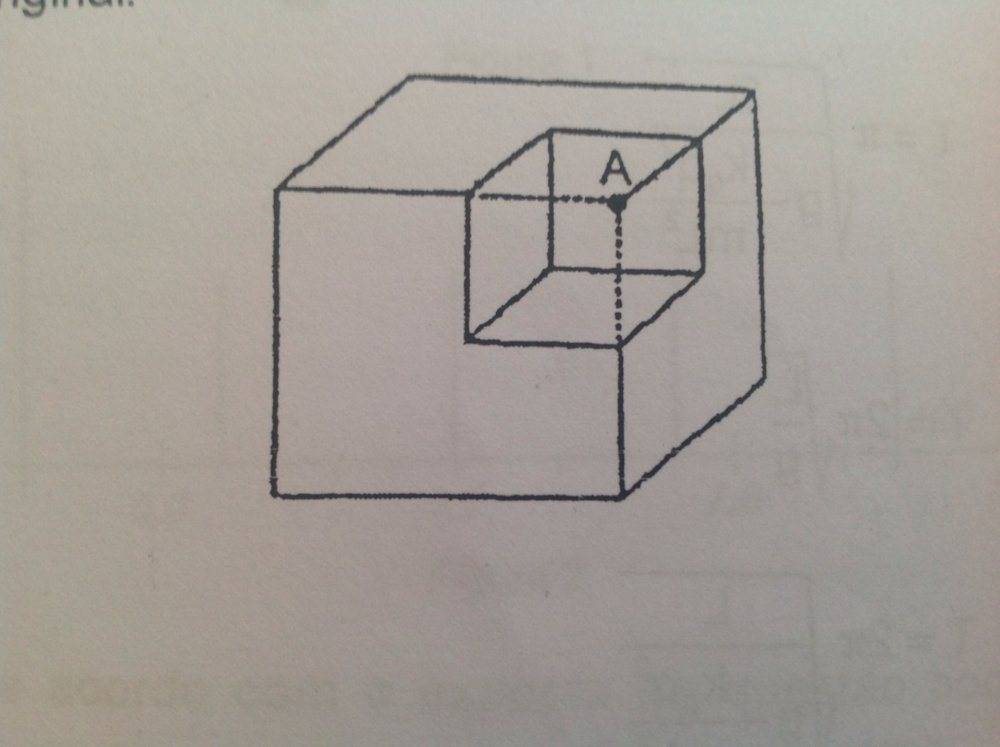
The discussion centers on calculating the electric field at a point A due to a uniformly charged cube with side length 'a' and volumetric charge density. Participants explored the challenges of applying Gauss's Law due to the lack of symmetry and the complexity of integrating the electric field contributions from the cube's charge distribution. They concluded that using the principle of superposition and comparing the effects of a smaller cube with opposite charge density can yield insights into the relationship between electric field strength and cube dimensions. The final consensus is that the electric field strength is proportional to the charge density and inversely related to the distance from the center of the cube.
PREREQUISITES
- Understanding of Gauss's Law in electrostatics
- Familiarity with electric field calculations using integration
- Knowledge of the principle of superposition in electric fields
- Basic concepts of charge density and its effects on electric fields
NEXT STEPS
- Study the application of Gauss's Law for different charge distributions
- Learn about electric field calculations for various geometries, including cubes and spheres
- Explore the concept of electric field superposition in more complex charge arrangements
- Investigate the relationship between charge density and electric field strength in electrostatics
USEFUL FOR
Physics students, electrical engineers, and anyone interested in electrostatics and electric field calculations will benefit from this discussion.
 ##\qquad## !
##\qquad## ! 