Tony Hau
- 107
- 30
- Homework Statement
- A primitive model for an atom consists of point molecules ##(+q)## surrounded by a uniformly charged spherical cloud ##(-q)## of radius ##a## (Fig.1). Calculate the atmoic polarizability of such an atom.
- Relevant Equations
- ##E_{dip}(r,\theta) = \frac {p}{4 \pi \epsilon_o r^{3}}(2cos(\theta)\hat {\mathbf r} + sin(\theta) \hat {\mathbf \theta}) ##
The question is like this:
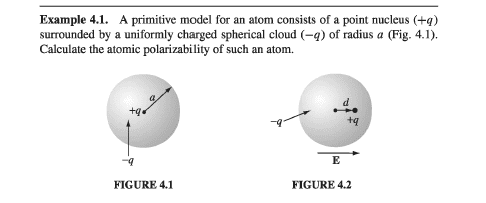
The solution is like this:
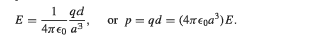
However, according to the equation for ##E_{dip}## , what I think is that it should be: $$E=\frac {1}{4 \pi \epsilon_o} \frac {qd}{d^3} \hat {\mathbf z} $$, where I take the centre of the sphere in figure 2 as the centre of the coordinate, and positive z-axis towards right.
Actually it doesn't have to be that complicated. The electric field experienced by the positive charge on the left in figure 2 can be simply calculated by the Coulomb's law ##E=\frac{1}{4 \pi \epsilon_o}\frac{-q}{r^2}##. Anyway, I don't know why the textbook gives something different.
The solution is like this:
However, according to the equation for ##E_{dip}## , what I think is that it should be: $$E=\frac {1}{4 \pi \epsilon_o} \frac {qd}{d^3} \hat {\mathbf z} $$, where I take the centre of the sphere in figure 2 as the centre of the coordinate, and positive z-axis towards right.
Actually it doesn't have to be that complicated. The electric field experienced by the positive charge on the left in figure 2 can be simply calculated by the Coulomb's law ##E=\frac{1}{4 \pi \epsilon_o}\frac{-q}{r^2}##. Anyway, I don't know why the textbook gives something different.
Last edited: