Winzer
- 597
- 0
Homework Statement
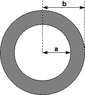
A long cylindrical insulating shell has an inner radius of a = 1.38 m and an outer radius of b = 1.61 m. The shell has a constant charge density of 4.80 C/m3.1. What is the magnitude of the electric field at a distance of 1.87 m from the axis?
2. What is the magnitude of the electric field at a distance of 1.51 m from the axis?
3. If we take the potential at the axis to be zero, what is the electric potential at the outer radius of the shell?
Homework Equations
E=\frac{kq}{r^2}
\oint \vec{E}\vec{dr}= \frac{Q_{Enclosed}}{\epsilon_{o}}
The Attempt at a Solution
For 1 i use E=\frac{kq}{r^2} but i am confused on finding q because i am given density of c/m^3. I am assuming an infinity long cyclinder?\vec{}