Electric Flux Through the Surface of a Circle

[TerraForce469]

Homework Statement

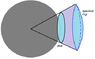
A sphere of radius $R$ carries charge density $\rho = ar^5$ where $a$ is a constant. Find the flux $\Phi$ of its electric field through a surface of a circle with radius $R$ if the circle lies in a plane tangent to the sphere and its center touches the sphere.

Homework Equations

Gauss' law to calculate $\vec{E}$ of the charged sphere: $$\oint \vec{E}\cdot d\vec{A} = \frac {Q_{enc}}{ε_0}$$

The total charge of the sphere (assuming volumetric charge density, wasn't specified which type in the original prob.): $$ Q_{enc} = \int_V \rho(r)\,dV $$

And of course, the electric flux: $$ \Phi_E = \int \vec{E}\cdot d\vec{A} $$

The Attempt at a Solution

I found total charge enclosed by integrating all over the volume of the sphere and obtained: $$ Q_{enc} = \frac{1}{2} \pi a R^8 $$

Then I used Gauss' law to find $\vec{E}$ and obtained: $$ \vec{E} = \frac{aR^8}{8ε_0r^2} \hat{r} $$

The surface over which I wanted to find the flux, take it to be at the right of the sphere and touching it at its center. I will call its differential area $dA' = r' d r' d \theta$.

The only contributions of $\vec{E}$ come from its component normal to $\vec{dA'}$. Thus we need to find the magnitude corresponding to that component using: $$ cos(α) = \frac{R}{r} $$ where $r= \sqrt{r'^2 + R^2}$. I apologize if you cannot visualize it or understand how I am approaching this, but bear with me. Basically α is the angle between the radius $R$ of the sphere and $r$, the distance of the $\vec{E}$ component.

So now I take the flux:

$$ \Phi_E = \int_S \vec{E}\cdot d\vec{A'} = \int_S E cos(α) dA' $$

And then substitute in my previous expressions for $E$ and $cos(α)$, and integrating all over the flux surface:

$$ \Phi_E = \int_0^{2\pi} \int_0^R (\frac{aR^8}{8ε_0r^2})(\frac{R}{r}) r' dr' d \theta' = \int_0^{2\pi} \int_0^R (\frac{aR^8}{8ε_0(r'^2 + R^2)})(\frac{R}{\sqrt{r'^2 + R^2}}) r' dr' d \theta' $$

(I don't know how to write the equation in steps using Latex, if someone could please inform me how to on the forums that would be appreciated). My final solution is:

$$ \Phi_E = \frac{\pi a R^8}{4ε_0} (1 - \frac{1}{\sqrt{2}}) $$

I was hoping to check if my methodology was correct and if I am doing something wrong. This problem took me a while to do and I want to at least check that it seems proper. Feel free to ask and I will clarify. Thank you!

 

[TSny]

Hi TerraForce469.

Your work looks correct to me. Nicely done!

 

[Saitama]

Hi TerraForce469.

Your work looks correct to me. Nicely done!

Hi TSny!

I was wondering if there is any elegant solution to this problem. I am not sure but can we use the spherical cap method you taught me recently?

EDIT: That seems to work, I should have tried it before posting the reply.

 

[TSny]

Hi Pranav-Arora.

Yes! TerraForce469's write-up was so nicely done that I didn't even think about another way.

You can easily check that it will yield the correct answer without doing any flux integration (if you know or look up the formula for the solid angle of a cone in terms of its apex angle.) Of course you still need to do the integral to get the total charge.

Thanks for reminding me.

 

[TSny]

Terraforce469,

If you want to try Pranav-Arora's suggestion, then extend the radial lines from the center of the sphere through the edge of the disk to produce a cone. Then cap the cone with a spherical cap that is part of a sphere centered on the center of the charged sphere. Compare the flux through the disk with the flux through the spherical cap.

[You don't need to extend the radial lines, you could just cap the disk with a spherical cap.]

 

[TerraForce469]

Pranav-Arora and TSny,

Sorry I couldn't respond any sooner; quite a busy day I had today.

Thank you for your responses! Although we are supposedly still at rudimentary work, it's reassuring to know that the solution to a difficult problem is correct when I good critical reasoning of fundamental relevant concepts are applied.

At a glance, the spherical cap method does seems more intuitive. I can see how the flux through the spherical cap is equivalent to that of the disk. However, what changes from my original approach? Is that the solid angle of the spherical cap is taken into account?

 

[TSny]

At a glance, the spherical cap method does seems more intuitive. I can see how the flux through the spherical cap is equivalent to that of the disk. However, what changes from my original approach? Is that the solid angle of the spherical cap is taken into account?

Yes. The field is radial and has uniform magnitude over the surface of a sphere centered on the charge distribution. So, the flux through a spherical cap is just the magnitude of the field times the area of the cap.

The area of the cap is $r^2\Omega$ where $\Omega$ is the solid angle subtended by the cap.

$r^2$ cancels out when multiplying the area by the field since E varies as $1/r^2$ outside the charge distribution.