Electric Potential and bounds of integration

[timmastny]

Homework Statement

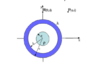
Find the potential difference between V(P) - V(R) and V(c) - V(a)

Homework Equations

Electric potential:

V(a) - V(b) = \int^{b}_{a}E*dr

V(b) - v(a) = -\int^{a}_{b}E*dr

Fundamental Theorem of Calculus:

F(b) - F(a) = \int^{b}_{a}f(x)dx

The Attempt at a Solution

My question is about the solutions attached. In the first example, we have V(P)-V(R), which makes the integral \int^{R}_{P}E*dr. However, when evaluating the integral, the solution takes V(P)-V(R) which seems to disagree with the fundamental theorem of calculus. As per the bounds, I think it should be V(R)-V(P).

Note: while I think it is wrong, the online homework said that evaluting it V(R)-V(P) is incorrect.

Likewise, to add to the confusion, the second picture is the solution for V(c)-V(a), which makes an integral \int^{a}_{c}E*dr. In this case, though, the solution is found by taking v(a)-v(c). (technically v(a) - v(b) because v(c)-v(b) is a constant). This result seems to follow the fundamental theorem of calculus and is the result I expected.

Finally, I thought maybe it had to do with the geometry so I attached a picture of the scenario. Hopefully some one can shed some light on the confusing integral bounds. Thanks

 

[rude man]

Homework Statement

Find the potential difference between V(P) - V(R) and V(c) - V(a)

Homework Equations

Electric potential:

V(a) - V(b) = \int^{b}_{a}E*dr

.

No. V(b) - V(a) = -∫E*dr with lower limit of r(a) and upper limit of r(b), with * denoting the vector dot-product. If a unit test charge is moved from a to b where r(a) > r(b) then this integral is positive and represents both the gain in potential and the work done in moving a unit test charge from a to b.

OK, yor formula is not wrong quantitatively but you should think of going from a to b as integrating from a to b, and that means V = -Edr.

 

[rude man]

Homework Statement

Find the potential difference between V(P) - V(R) and V(c) - V(a)

Homework Equations

Electric potential:

V(a) - V(b) = \int^{b}_{a}E*dr

V(b) - v(a) = -\int^{a}_{b}E*dr

This is a contradiction in terms!