Electrical analog and impedance

Click For Summary
SUMMARY

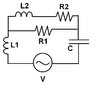
The discussion focuses on the relationship between mechanical systems and electrical circuits, specifically through the lens of impedance and differential equations. Participants analyze the damping forces on two masses, m1 and m2, and relate them to electrical components using an electromechanical analogy. Key formulas discussed include the conversion of mechanical quantities to electrical equivalents, such as q ~ x, i ~ v, k ~ 1/C, L ~ m, and b ~ R. The impedance is calculated from the equivalent circuit formed by these relationships, emphasizing the importance of understanding both the physical and mathematical aspects of the problem.

PREREQUISITES
  • Understanding of differential equations in mechanical systems
  • Familiarity with electromechanical analogies
  • Knowledge of electrical circuit components (resistors, inductors, capacitors)
  • Basic principles of impedance in AC circuits
NEXT STEPS
  • Study the derivation of impedance in complex form: Z_R = R, Z_L = jLω, Z_C = -j/(Cω)
  • Learn about the electromechanical analogy in detail, focusing on mass-spring-damper systems
  • Explore circuit analysis techniques for combined series and parallel RLC circuits
  • Review differential equations related to mechanical systems and their electrical counterparts
USEFUL FOR

Students and professionals in physics and engineering, particularly those specializing in electrical engineering, mechanical systems, and circuit analysis.

Shackleford
Messages
1,649
Reaction score
2
I'm a bit lost on this one. Also, what formula do I use for impedance?

http://i111.photobucket.com/albums/n149/camarolt4z28/2010-09-19202315.jpg?t=1284947003

http://i111.photobucket.com/albums/n149/camarolt4z28/2010-09-19202817.jpg?t=1284947014
 
Last edited by a moderator:
Physics news on Phys.org
What are the differential equations for m1 and m2? Notice that now the damping force on m1 is -b_1(\dot{x}_1-\dot{x}_2) (that is, it depends on the RELATIVE velocity between the masses).
After write down the 2 equations, relate it to an electrical circuit by using electromechanics analogy:
q ~ x
i ~ v (or dx/dt)
k ~ 1/C
L ~ m
b ~ R
Fcos(wt) ~ Vcos(wt)

The impedance is calculated from the circuit built :smile:
 
hikaru1221 said:
What are the differential equations for m1 and m2? Notice that now the damping force on m1 is -b_1(\dot{x}_1-\dot{x}_2) (that is, it depends on the RELATIVE velocity between the masses).
After write down the 2 equations, relate it to an electrical circuit by using electromechanics analogy:
q ~ x
i ~ v (or dx/dt)
k ~ 1/C
L ~ m
b ~ R
Fcos(wt) ~ Vcos(wt)

The impedance is calculated from the circuit built :smile:

That makes sense. The problem doesn't imply they move with the same velocity. That's why I was adding the masses.

Actually, the damping force on m2 is -b_2(\dot{x}_2). I'll write out the DEs tomorrow. I'm tired. Thanks for the help.
 
Last edited:
Are my equations correct? If so, do I then start substituting the electrical analogs? If so and assuming I get that correct, I'm not sure what to do after that. I suppose I could find my electrical solutions and then plug those into the impedance formula (whatever that is).

http://i111.photobucket.com/albums/n149/camarolt4z28/2010-09-22220323.jpg?t=1285211103
 
Last edited by a moderator:
It's not correct, because you forgot the elastic force F=-kx :biggrin:
Well, the next thing to do is to convert these into an equivalent circuit :smile: Just replace F with V, k with 1/C, etc, and what you get is 2 voltage equations. You will then know what to do.
 
hikaru1221 said:
It's not correct, because you forgot the elastic force F=-kx :biggrin:
Well, the next thing to do is to convert these into an equivalent circuit :smile: Just replace F with V, k with 1/C, etc, and what you get is 2 voltage equations. You will then know what to do.

Crap. I knew I was forgetting something. I was pretty tired last night. Let me re-write this. It's absolutely important that I firstly understand the situation physically then construe it mathematically.

However, I have a question. The mass m1 has the spring restoring force, but the mass m2 does not. M2 has the frictional force from the floor based on its velocity and then again the force of friction from m1.
 
The mass m1 has the spring restoring force, but the mass m2 does not. M2 has the frictional force from the floor based on its velocity and then again the force of friction from m1.

Yes, you're right :smile:
But... is that a question? :rolleyes:
 
hikaru1221 said:
Yes, you're right :smile:
But... is that a question? :rolleyes:

Haha! Oops.

Okay, I'll give you a question now. Is this correct?

http://i111.photobucket.com/albums/n149/camarolt4z28/2010-09-23191532.jpg?t=1285288944
 
Last edited by a moderator:
Your equations are correct.
 
  • #10
hikaru1221 said:
Your equations are correct.

Hey, that's great. Now, I can attempt my electrical analogs. However, should I write it in terms of I or q? And, isn't impedance equal to the square root of the sum of the squares of RL and RC. I vaguely remember the equation.
 
  • #11
Just do as I suggested earlier. Convert all the mechanical quantities into the equivalent electrical quantities, and you have 2 voltage equations. Each term of the voltage equations corresponds to a device (L, R, C, source). From the equation, you can draw the equivalent circuit and then from the circuit, calculate the impedance.
 
  • #12
hikaru1221 said:
Just do as I suggested earlier. Convert all the mechanical quantities into the equivalent electrical quantities, and you have 2 voltage equations. Each term of the voltage equations corresponds to a device (L, R, C, source). From the equation, you can draw the equivalent circuit and then from the circuit, calculate the impedance.

Here are my equations. One of my classmates was saying something about the delta-q being the current through the R1 resistor or something like that. Each of these terms has to be voltage.

http://i111.photobucket.com/albums/n149/camarolt4z28/2010-09-25172307.jpg?t=1285453923
 
Last edited by a moderator:
  • #13
You're on the right track. Take your friend's hint, replace \ddot{q} with \frac{di}{dt} and \dot{q} with i; you will see it clearer. And yes, each term corresponds to voltage across some electrical device.

P.S.: I saw the term corresponding to kx_1 is a bit incorrect.
 
  • #14
hikaru1221 said:
You're on the right track. Take your friend's hint, replace \ddot{q} with \frac{di}{dt} and \dot{q} with i; you will see it clearer. And yes, each term corresponds to voltage across some electrical device.

P.S.: I saw the term corresponding to kx_1 is a bit incorrect.

Ah. You're right. I accidentally put the dot over the q. Let me see what I can come up with. I took Physics II two years ago. That's the last time I really dealt with impedance, circuits, and so forth.

http://i111.photobucket.com/albums/n149/camarolt4z28/2010-09-25233241.jpg?t=1285475708
 
Last edited by a moderator:
  • #15
The last term of 2nd equation is a bit incorrect. Anyway, from here, can you build a corresponding circuit?
 
  • #16
hikaru1221 said:
The last term of 2nd equation is a bit incorrect. Anyway, from here, can you build a corresponding circuit?

Crap. I put the dot somewhere but not where it belonged!

The circuit has two inductors, two resistors, and on capacitor. Does it have a parallel branch?
 
  • #17
Yes. That's why I told you to replace q' with i :smile: There should be some parallel branches. Hint: You can rewrite the 2nd equation as R_1(i_1-i_2)=L_2\frac{di_2}{dt}+R_2i_2 so that you can see a common term of both equations. That shows something about the parallel branches.
 
  • #18
hikaru1221 said:
Yes. That's why I told you to replace q' with i :smile: There should be some parallel branches. Hint: You can rewrite the 2nd equation as R_1(i_1-i_2)=L_2\frac{di_2}{dt}+R_2i_2 so that you can see a common term of both equations. That shows something about the parallel branches.

Unfortunately, I don't have a damn idea what to do or how to calculate the impedance. I suppose I could insert the common term into equation one, but I don't see how that helps me. I guess I first need to know how I can calculate the impedance then try to see how my equations could get me there.
 
  • #19
Well you must first build the equivalent circuit :smile: There is no way around I suppose.
You don't have to substitute the common term into the 1st equation. Let me explain the circuit for you.
_ From the 1st equation: L_1\frac{di_1}{dt}+R_1(i_1-i_2)+\frac{q_1}{C}=V

That is, there is a source V, connected in series with an inductor L1, a resistor R1, a capacitor C. If you look at the current accompanying each term, you can see that L1 is accompanied by I1 and C is accompanied by Q1 which is directly related to I1. However, R1 is accompanied by (I1 - I2), i.e. the current through R1 is only a part of I1. Therefore there must be something connected in parallel to R1.

_ Indeed, the 2nd equation shows so: R_1(i_1-i_2)=L_2\frac{di_2}{dt}+R_2i_2

We can see that, sharing the same voltage as R1, there is a branch consisting of L2 and R2, both of which are accompanied by I2.

So now can you draw the equivalent circuit? :wink: From the circuit, you can easily find the impedance.
 
  • #20
That makes sense.

This is probably wrong, but it kind of makes sense since this in this electrical analog the voltage source would provide AC.

Edited for embarrassment.
 
Last edited:
  • #21
Sorry, it's really wrong :rolleyes:
Remember that the branch (L2 and R2) is parallel to R1. Besides the source has 2 terminals.
 
  • #22
hikaru1221 said:
Sorry, it's really wrong :rolleyes:
Remember that the branch (L2 and R2) is parallel to R1. Besides the source has 2 terminals.

What the heck did I just write. That's not a circuit. I'm multitasking here, so let me redo that. -_-

Okay, here it is.

http://i111.photobucket.com/albums/n149/camarolt4z28/2010-09-26162147.jpg?t=1285536201
 
Last edited by a moderator:
  • #23
What you drew is that the branch (L1 + C), not R1, is parallel to (L2 + R2)!
 
  • #24
hikaru1221 said:
What you drew is that the branch (L1 + C), not R1, is parallel to (L2 + R2)!

I thought the difference in current indicated a parallel circuit going into R1.
 
  • #25
http://i111.photobucket.com/albums/n149/camarolt4z28/2010-09-26164217.jpg?t=1285537508

Wait. I see what you're saying now. Hold on.
 
Last edited by a moderator:
  • #26
Now you got it. Then calculate the impedance from the circuit.
 
  • #27
hikaru1221 said:
Now you got it. Then calculate the impedance from the circuit.

So, my terminals are correct?

If I'm looking at this the right way, there's one charge going "directly" through R1 and then the "other" charge going through L2 and R2. Those two charges constitute the I1 current through the R1, L1, and C series.
 
  • #28
What's with "charges"? You mean "current"?
 
  • #29
hikaru1221 said:
What's with "charges"? You mean "current"?

Yes. Current is simply the movement of the "charges" with respect to time.
 
  • #30
Let me redraw the circuit in the standard way. See the picture attached.
Now can you calculate the impedance from the circuit?
 

Attachments

  • untitled.JPG
    untitled.JPG
    18.8 KB · Views: 432

Similar threads

How Do Transition Wavelengths Compare Between Hydrogen and Helium?
  • · Replies 3 ·
Replies
3
Views
2K
Radial Wave Function: Solving Equation for Normalized Radial Wave Function
  • · Replies 12 ·
Replies
12
Views
7K
Modern Optics: Polarization/Jones Vectors
  • · Replies 2 ·
Replies
2
Views
2K
Minimize surface area - calculus of variations
  • · Replies 2 ·
Replies
2
Views
2K
Show eigenvalues of hermitian operator are real
  • · Replies 13 ·
Replies
13
Views
10K
Kepler's Third Law and centripetal acceleration
  • · Replies 2 ·
Replies
2
Views
2K
If A and B are hermitian, then i[A,B] is also hermitian
  • · Replies 17 ·
Replies
17
Views
10K
Find the normalized eigenspinors of the 2 x 2 matrix
  • · Replies 9 ·
Replies
9
Views
7K
What is the value of N when evaluating the integral for thermal photons?
  • · Replies 2 ·
Replies
2
Views
2K
Projectile Motion: Launching Up a Hill
  • · Replies 9 ·
Replies
9
Views
3K