Electronics: Plot Vout of RC circuit

[oddjobmj]

Homework Statement

http://imgur.com/OowiMCR

As noted in the image:

In the circuit below, R₁=R₂=10kΩ, and C=0.1μF. Plot V_out(t) if the input, V_in, is a step function of height V₀ at t=0

Homework Equations

V_cap=V₀-Ce^-t/RC

The Attempt at a Solution

I was hoping someone could explain what is actually going on in that circuit.

I understand the general idea of a capacitor. At t=0 the charge stored by the capacitor is 0 and as time goes on it gains charge. After long t it will be fully charged and there won't be a potential difference between the capacitor and the source so the current will go to 0.

I'm just not sure how to read this diagram. It looks nothing like what I have seen. Can I interpret the grounds along the bottom to be connected?

Thank you for your help!

 

[BvU]

Yes you can. Earth is considered to be at zero potential.
Let me caution you that the Vo in your expression is the voltage over the capacitor at time t=0, whereas in the drawing it is the height of the jump in Vin at t=0.
You have one R in the expression and two in the diagram. You'll have to go back to the section where the expression was derived to find out what to do with R1 and R2

 

[oddjobmj]

Thank you BvU.

You have one R in the expression and two in the diagram. You'll have to go back to the section where the expression was derived to find out what to do with R1 and R2

This is what I'm asking about, mostly. The diagram doesn't make sense to me. The derivation in the book looks at a circuit with a single resistor and nothing more that I can find.

A few specific questions come to mind with regard to the diagram:

Why is Vout on the side opposite Vin? Why are there gaps where Vin and Vout are noted? What do I do with a resistor in parallel with the capacitor? It doesn't seem as simple as using the R_eq in place of the two resistors.

 

[BvU]

At the risk of offending some electronicos: they like simple diagrams that make sense when read from left to right.

You can think of the open circles left and right as sockets for simple so-called banana plugs. On the right we connect a voltmeter (or something equivalent that doesn't disturb the experiment). On the left we stick in a battery at t=0 and that's the start of the experiment.

The derivation in the book probably sets up a differential equation using Q = CV and I = dC/dt.
Ask yourself what currents flow in R1, R2, C and what their effect is on the voltages over each.
Perhaps you can adapt some chunks of the derivation in the book and put them to good use !

 

[oddjobmj]

Ahh, thanks again!

Would this be a reasonable way to think of the circuit?

http://imgur.com/1JJszNv

(Beautiful, I know!)

So at small t the capacitor is charging and drawing all of the current because it acts much like a short circuit. Is it safe to say that all of the current goes through the capacitor until it is fully charged?

After it is charged it acts like an open circuit so all of the current is redirected through the resistor in parallel with the capacitor.

We have no switch to discharge the capacitor unless we simply remove the voltage source which would discharge the capacitor through the resistor it is in series with.

 

[BvU]

Drawing is a beauty indeed!

So at small t the capacitor is charging and drawing all of the current because it acts much like a short circuit. Is it safe to say that all of the current goes through the capacitor until it is fully charged?

Nope. It is safe to say that all of the current goes through R1, though...

After it is charged it acts like an open circuit so all of the current is redirected through the resistor in parallel with the capacitor.

Unfortunately: close, but nope. Things happen simultaneously. Fortunately, you know the relationship between current and voltage for R2 and also for R1 and also for C (where you need a time derivative)

We have no switch to discharge the capacitor unless we simply remove the voltage source which would discharge the capacitor through the resistor it is in series with.

True. Before t=0 the voltage source was at V=0, so the C could discharge over R1 and R2 in parallel.
Removing the voltage source indeed let's C discharge over R2.

 

[oddjobmj]

Ah, in that case I have no idea where to go from here.

All I can think to do is find the equivalent resistance of the two parallel resistors and use that to find the total current. Then I can find the voltage drop across R1 and use the remaining voltage on each R2 and the capacitor.

Do I look at this like a voltage splitter with the second resistor (the capacitor) changing over time?

 

[BvU]

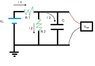
To get you going, let's assume you have named the various items in your drawing as in the accompanying picture.

(By the way, you get more standing in the electronico's world if you draw a voltmeter as a V in a circle. You've seen that drawing a resistance this way is tedious. Electronicos are just like people, they want things simple, so they usually draw a rectangle - but in this case the book uses a zig-zag wire, so we stick to that).

The idea is to collect enough relations between them that you can solve for the unknown Vout as a function of t. This is where the template comes in so handy!

R1=R2=10kΩ, and C=0.1μF. Plot Vout(t) if the input, Vin, is a step function of height V0 at t=0

So Vout(t) is the unknown we are after. For the moment we don't know I1, I2 and I3, but I am quite sure you can make that step on your own (listing a few relations between knowns and unknowns). If all is well, you end up with a solvable set of equations.

--

... with the second resistor (the capacitor) changing over time

This made some alarm bells go off, so I'll expand a little here:
The first part of the sentence is dead on, so no problem there. But it is dangerous to even think of a capacitor as a kind of weirdo resistor. Brrrr. Big warning signs, flashing lights, bells and sirens!

Reason: A resistor is like friction: work is dissipated into heat. A capacitor is more like a charge bottle: you can store it and get it back later. The more you store, the higher the voltage (like pressure if it were a gas bottle). Some joker can hand you a charged capacitor and if you touch both wires you get a shock. With a resistor all that can be pranked is that they heat it up and hand it to you quickly (well, that wasn't a very didactical example...)

Other reason: you scare me into thinking you see parallel resistors.

But remember, the first part of the sentence quoted is right. If in doubt, go back to where that R-only voltage divider was treated. See also post #4.

Your turn. Good luck!