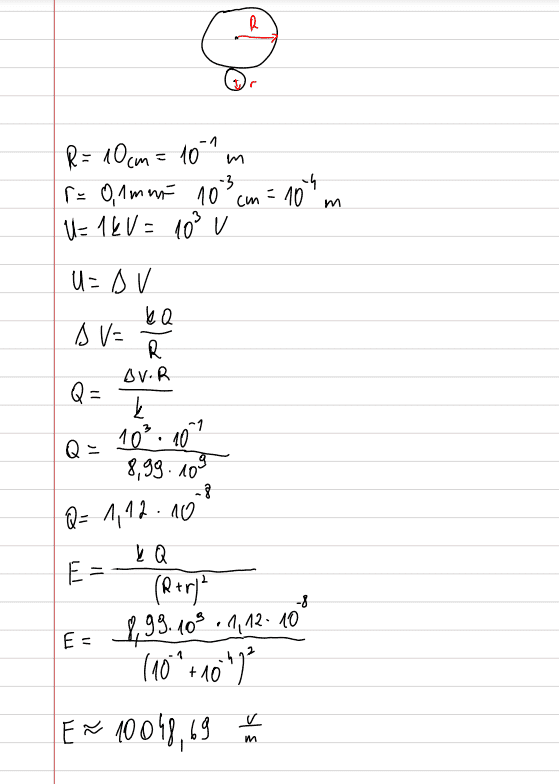SUMMARY
The discussion centers on solving an electrostatics problem involving two charged spheres, one larger and one smaller, with the larger sphere being conductive. The participants clarify that if both spheres are conductive, charge will redistribute until they reach the same potential. The correct approach involves using the equations for electric potential, specifically ##V_1 = K\frac{Q-Q_2}{R}## for the larger sphere and ##V_2 = K\frac{Q_2}{R_2}## for the smaller sphere, with the total charge being the sum of both spheres' charges. The final potential of the larger sphere is given as 10 kV, which is critical for determining the charge distribution.
PREREQUISITES
- Understanding of electrostatics principles, particularly charge distribution.
- Familiarity with electric potential equations, specifically ##V = K\frac{Q}{R}##.
- Knowledge of conductive materials and their behavior in electrostatic scenarios.
- Ability to solve systems of equations involving electric charge and potential.
NEXT STEPS
- Study the principles of electrostatic induction and its effects on charge distribution.
- Learn about the behavior of conductive materials in electrostatic fields.
- Practice solving electrostatics problems involving multiple conductive objects.
- Explore the concept of electric potential and its applications in circuit analysis.
USEFUL FOR
Students of physics, electrical engineers, and anyone interested in understanding electrostatics and charge interactions between conductive materials.