Energy landscape in the two state model (Boltzmann distribution)

[MikeGG]

Homework Statement

Draw an energy landscape such as shown in Figure 7.7 for
the voltage-gated sodium channel presented in Figure 7.2.
In particular, show how the landscape changes as a function
of the applied voltages shown in Figure 7.2(C).

Relevant Equations

E(σ ) = σ εopen + (1 − σ )εclosed − στA

Gtension = − τΔs × (R /Rout)× ΔR × (2πRout/s)

Gtension = −τ2πRΔR

ΔΑ= 2πRΔR

Popen = e^−β(εopen−τΔA) /(e^−β(εopen−τΔA) + e^−βεclosed)

β=1/ ΚΤ

From an excel file I can get the probability of each energy state Εi and I saw at Wikipedia that the probability of each energy is proportional with

e^−Εi/KT, from this I find the energy of every micro state. Also from the formula

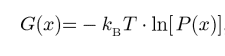which I found on a paper I can get a curve like the curve shown in fig7.7 (almost) whith the probabilities I took.

My problem is that it must be an energy as a function of the Radius, so I must put in there somehow the R. I can take the formula with Popen and to put on the denominator all of the energies and on the numerator the energy of each microstate but then I don't have the R.
If i put the whole energies of each state I could put ΔΑ but i don't see how with that I could made curves like fig7.7 and also instead of τ I must put v (volts), the probabilities I took was from -105 mVolts, if I put that the result doesn't makes sense.

So I want the different probabilities to use the formula

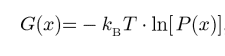but I can't find a way to put radius in. That's the way I am thinking it, I would appreciated if someone could tell me if I am in the right direction and maybe give a hint how to move forward or to give me a hint for another direction.
Also, fig 7.2 has the Δε which indicates the it may be useful for the drawing of the energy landscape but I can't figure out how.

Thanks

 

[Nate810]

in advance!It seems like you have a good start, but I'm not sure if this approach will work for what you're trying to do. One suggestion might be to try and find a way to relate the radius to the energy states. For example, if you know the size of each energy state and the radius, you could then use that information to calculate the energy of each microstate. You could then use this information to construct your energy landscape, plotting energy against radius. Another suggestion would be to look up the Boltzmann Distribution equation, which gives the probability of occupancy of an energy state as a function of temperature. This equation should also let you incorporate the radius into your plot. Hope this helps!