Energy of an electron at rest?

[K.Callaghan]

An electron rest mass in kilograms is calculated from the definition of the Rydberg constant R∞:

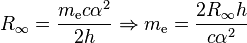
where α is the fine structure constant and h is simply Plancks constant. Now, assuming the electron has an associated rest energy, Any idea on how this is calculated? I'm assuming using relativistic means...but of what nature? Any thoughts? Formulas? Ideas?...

 

[Topolfractal]

Use E = mc^2 with m being the rest mass of the electron

 

[K.Callaghan]

Thank you for responding! Yes of course, of which I assume would be the easy answer. My concern is more of where this relationship has mechanical meaning... Which is to say what other formulas explain this relationship...this energy = mass light squared? Is there an equivalent? Can anyone explain in lamen terms why a particle at rest has energy other than to say it has "quantum behaviour"?

 

[Topolfractal]

Please can you explain more on what you mean by quantum behavior. Also there is another formula E^2=m^2 c^4 + p^ 2 c^2 which when p=0 reduces to e= mc^2. The proof of e= mc ^2 is,... ( A good proof is on the you tube channel minute physics).

 

[K.Callaghan]

Please can you explain more on what you mean by quantum behavior. Also there is another formula E^2=m^2 c^4 + p^ 2 c^2 which when p=0 reduces to e= mc^2. The proof of e= mc ^2 is,... ( A good proof is on the you tube channel minute physics).

--------
Sure. I'm not doubting whether the proof is sound, yet rather searching for another explanation for this relationship other than mass displays energy in states of "quanta", or as a wave function... As we know an electron exhibits both paticle and wave like characteristics... Such is what we would call quantum like behaviour. However such behaviour is usually calculated using multiple systems of momenta rather than a single particle at rest which essential to my understanding still has an associated energy, frequency, and wavelength...

 

[ChrisVer]

so you want a proof of R_\infty = \dfrac{m_ec \alpha^2}{2h}?

 

[Topolfractal]

No I don't want a proof of that , but thank you for offering. Now it sounds like you are trying to prove a relativistic formula quantum mechanically. The proof though in that video has nothing to do with quantization and proves it using the relativistic Doppler effect. He equates the doppler shifted perspective and the stationary perspective from energy conservation.

 

[Topolfractal]

My last message is to Callaghan sorry I should have quoted, and the first sentence to Chris ver

 

[K.Callaghan]

My last message is to Callaghan sorry I should have quoted, and the first sentence to Chris ver

-----
Exactly. Although more specifically, when considering a rest particle with an associated E irrespective of multiple systems of momenta and of course it's relationship with C^2... And I appoloize as I am not familiar with the video you speak of ? From minute physics did you say?

 

[Topolfractal]

Yes minute physics ,and please can you teach me how to quote people.

 

[K.Callaghan]

Yes minute physics ,and please can you teach me how to quote people.

I'll will definitely check it out ! As far as quoting someone Its my understanding that when you hit reply the previous post is quoted automatically.

 

[K.Callaghan]

Although I am online via mobile thus the reply layout may be different if your on your computer.

 

[Topolfractal]

I'm on my iPad, please though can you teach me how to quote. It could very well still work. No for me it isn't quoted.

 

[K.Callaghan]

Instead of replying directly in the "have something to add?" Column. Tap on the last response and hit reply. It's my understanding that the quotes are highlighted automatically. Hope this helps.

 

[Topolfractal]

Although I am online via mobile thus the reply layout may be different if your on your computer.

Shsjsjsjsj

 

[Topolfractal]

Thank you

 

[Topolfractal]

Now minute physics yay or nay ( help or not )

 

[K.Callaghan]

Your welcome!

 

[Topolfractal]

--------
Sure. I'm not doubting whether the proof is sound, yet rather searching for another explanation for this relationship other than mass displays energy in states of "quanta", or as a wave function... As we know an electron exhibits both paticle and wave like characteristics... Such is what we would call quantum like behaviour. However such behaviour is usually calculated using multiple systems of momenta rather than a single particle at rest which essential to my understanding still has an associated energy, frequency, and wavelength...

Thank you for responding! Yes of course, of which I assume would be the easy answer. My concern is more of where this relationship has mechanical meaning... Which is to say what other formulas explain this relationship...this energy = mass light squared? Is there an equivalent? Can anyone explain in lamen terms why a particle at rest has energy other than to say it has "quantum behaviour"?

Your quantum thinking has inspired me to wonder if e= mc^2 can be derived from quantum mechanics.
Now the non - relativistic Hamiltonian would correspondingly equal zero from being stationary but considering a relativistic free Hamiltonian instead that takes in moving particles. The formula E^ 2 = m^2c^4+ p^2 c^2 can be quantized to produce such a Hamiltonian and reduces to e= mc^2 on p= 0. This isn't a proof of course but is the foundational insight to the Dirac equation.

 

[Topolfractal]

Now actually because traditional quantum mechanics is based from classical mechanics which doesn't contain e= mc^ 2 there is no such notion in traditional quantum mechanics and therefore it can't be derived or proven using that theory.

 

[Topolfractal]

Now minute physics yay or nay ( help or not )

 

[K.Callaghan]

Excluding the hamiltionain operator.

 

[ChrisVer]

No,relativistic quantum mechanics make use of E^2 - |\vec{p}|^2 c^2 =m^2 c^4 formula, it doesn't prove it. This formula is taken from special relativity alone and it's a frame independent combination of the frame dependent quantities E,\vec{p}.

Also there is no quantization of that formula either... from that formula you obtain the classical field lagrangian for (mainly) the Klein Gordon field (and maybe you can say something about the Dirac field too)... The quantization is then applied on the fields (when you impose [anti]commutator relations and insert the ladder operators or when you write the canonical [anti]commutation relations). In both cases the fields are the ones that get the quantized...

 

[Topolfractal]

Now actually because traditional quantum mechanics is based from classical mechanics which doesn't contain e= mc^ 2 there is no such notion in traditional quantum mechanics and therefore it can't be derived or proven using that theory.

Formulated appropriately is identical to what you just said.