Equation for circle points in 3D

[Nikkki]

TL;DR

Calculate the coordinates of consecutive points based on ABC points lying on a circle in 3D space

Hello,

I am trying to solve a problem and I would like to ask for help.

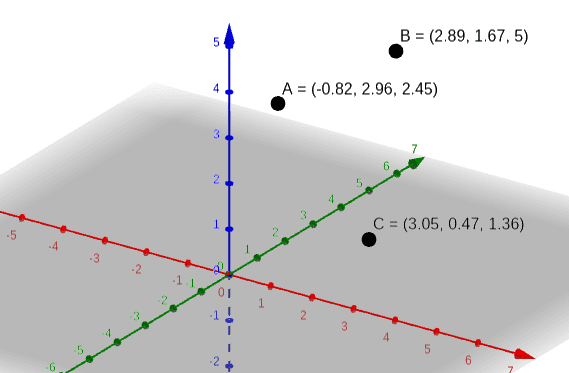
I have 3 points (A, B, C) in 3D space that are assumed to be on a circle.

EXAMPLE 1

EXAMPLE 2

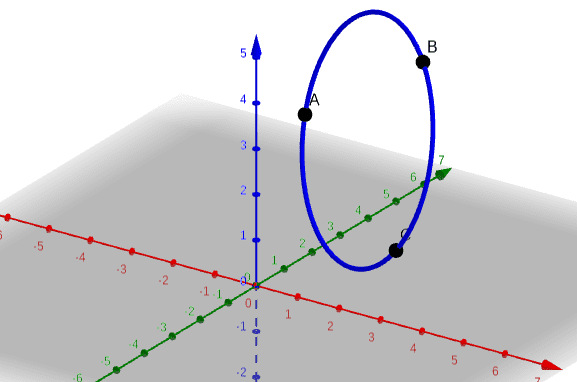
My goal is to create an algebraic formula to calculate the coordinates for 10 points on a circle composed of ABC points at any distance from each other.

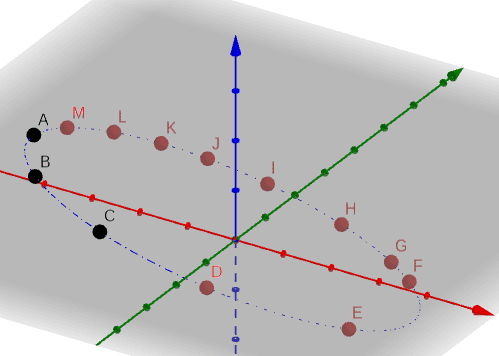
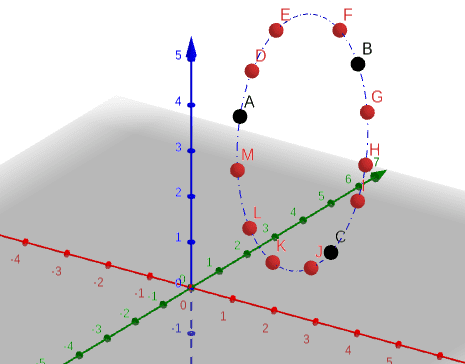
MY IDEA

My first idea was to create a triangle inscribed in a circle from the ABC points and then the radius of the circle.
First, I calculate the lengths of the triangle's legs by recalculating the lengths of |AB| |AC| and |CB| vectors.

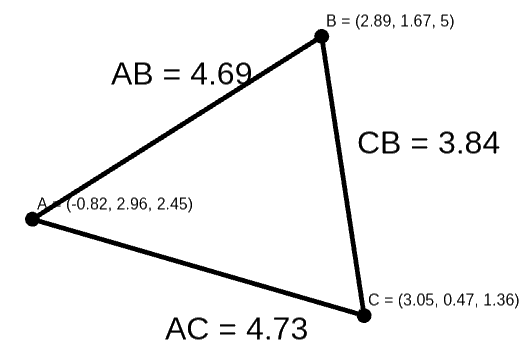
I calculate the radius length using the formula (https://www.physicsforums.com/threads/equation-of-a-circle-through-3-points-in-3d-space.173847/):

And at this step, I have now stopped

 

[mfb]

The center has a distance r to all these points. Can you find its coordinates as function of e.g. a, (b-a) and (c-a), e.g. the position of a and two sides? This is completely analogous to the two-dimensional problem.

 

[Nikkki]

The center has a distance r to all these points. Can you find its coordinates as function of e.g. a, (b-a) and (c-a), e.g. the position of a and two sides? This is completely analogous to the two-dimensional problem.

Thank you for your answer.
I am testing the formula for the circle center coordinates in the "Cartesian coordinates from cross- and dot-products" section on the website : https://en.wikipedia.org/wiki/Circu...sian_coordinates_from_cross-_and_dot-products

 

[jim mcnamara]

Hint: think bisector - the problem says 'lies on a circle' which has to imply that the points are not collinear.