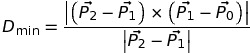MHB Formula for changing a plane intersection angle

[LMHmedchem]

Hello,

This is a bit more complex than my previous post, but I don't think it qualifies for university level difficulty. Please move this to the appropriate forum if my assessment is not correct.

I have 4 vectors in three space where each vector has its tail at the same point (point B).

id    x        y        z
B     0.000    0.000    0.000
vBA   0.183   -0.479    0.358
vBD   1.970    2.395   -0.524
vBE  -3.798   -1.214    0.168
vBC  -5.847    4.571   -1.137

I have the angle between each vector and vBC (in radians).

∠ ABC = 2.466
∠ DBC = 1.570
∠ EBC = 0.989

Each vector pair forming one of the angles above lies on a Euclidean plane. These planes intersect along vBC. I can calculate the plane intersection angles as follows.

For the intersection angle ∠ ABC ∩ DBC (angle of intersection between planes ABC and DBC, sorry I don't know the proper symbolic nomenclature for plane intersection angles).

1. take the vector rejection of vBA against vBC
2. take the vector rejection of vBD against vBC
3. calculate the angle between the two rejection vectors

∠ ABC ∩ DBC = 2.484
∠ ABC ∩ EBC = 0.674
∠ DBC ∩ EBC = 3.125

I need to change the angle of intersection between two planes without changing any of the angles between vectors ∠ABC, ∠DBC, or ∠EBC. Changing ∠ ABC ∩ DBC would involve essentially rotating the tip of vBA in a circle around the axis of vBC while the tail of vBA stays at point B, but I don't know how to do that.

The methods I have seem for rotating a vector in 3D involve rotating the vector about one axis.

From stackexchange, a 3D rotation around the Z-axis would be,

|cos θ   −sin θ   0| |x|   |x cos θ − y sin θ|   |x'|
|sin θ    cos θ   0| |y| = |x sin θ + y cos θ| = |y'|
|  0       0      1| |z|   |        z        |   |z'|

To use such a method, I would have to translate my current coordinates so that vBC is aligned with one axis, make the 3D vector rotation, and then translate back. That seems overly involved. It seems as if I should be able to use something like the above using the coordinates of vBC.

Any suggestions would be appreciated,

LMHmedchem

 

[MarkFL]

In this post:

http://mathhelpboards.com/calculus-10/12-3-63-determine-smallest-distance-between-point-line-22704-post102528.html#post102528

I showed that if we have a line described by the two points:

$$P_1\left(x_1,y_1,z_1\right),\,P_2\left(x_2,y_2,z_2\right)$$

And the point:

$$P_0\left(x_0,y_0,z_0\right)$$

Then the minimum distance between them is given by:

$$D_{\min}=\frac{\left|\left(\vec{P_2}-\vec{P_1}\right)\times\left(\vec{P_1}-\vec{P_0}\right)\right|}{\left|\vec{P_2}-\vec{P_1}\right|}$$

I would use this formula to determine the distance of the head of the vector to be rotated from the axis of rotation, and then use the formula again to determine the locus of points all having this same distance from both the fixed tail and the axis of rotation. You will likely get two circles, one of which would be discarded.

 

[LMHmedchem]

I showed that if we have a line described by the two points:

$$P_1\left(x_1,y_1,z_1\right),\,P_2\left(x_2,y_2,z_2\right)$$

And the point:

$$P_0\left(x_0,y_0,z_0\right)$$

Then the minimum distance between them is given by:

$$D_{\min}=\frac{\left|\left(\vec{P_2}-\vec{P_1}\right)\times\left(\vec{P_1}-\vec{P_0}\right)\right|}{\left|\vec{P_2}-\vec{P_1}\right|}$$

Looking at the equation above,

View attachment 7610

does the numerator refer to the cross product of vectors (p2-p1) and (p1-p0)? Since the resulting distance D_min is a scalar, it seems as if this should be a simple product, but "x" often means cross product when vectors are concerned so I thought I should ask. Since the shortest distance between the line and a point is a vector perpendicular to the line, the cross product also makes sense.

Sorry about not being very good with latex.

LMHmedchem

 

[MarkFL]

Looking at the equation above,

does the numerator refer to the cross product of vectors (p2-p1) and (p1-p0)? Since the resulting distance D_min is a scalar, it seems as if this should be a simple product, but "x" often means cross product when vectors are concerned so I thought I should ask. Since the shortest distance between the line and a point is a vector perpendicular to the line, the cross product also makes sense.

Sorry about not being very good with latex.

LMHmedchem

The numerator is the magnitude of the indicated vectorial cross product. :)