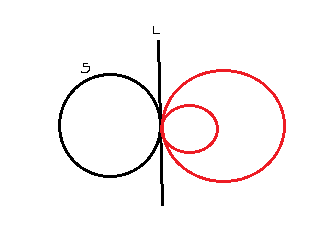Equation of family of circles

[AdityaDev]

In my textbook, its given that the equation of family of circles touching a given circle S and line L is $S+\lambda L=0$

So to find the equation of family of circles touching line L at point P(p,q), can i use the same equation taking S to be a circle of radius zero and center at P?
That is, if L is ax+by+c=0 and P is (p,q), then S will be $(x-p)^2+(y-q)^2=0$ and the equation of family of circles will be $(x-p)^2+(y-q)^2+\lambda (ax+by+c)=0$. Is this correct? such a circle passes through P.

 

[Mark44]

In my textbook, its given that the equation of family of circles touching a given circle S and line L is $S+\lambda L=0$

As it stands, this equation doesn't make sense to me. I don't know what it means to add a circle and a multple of a line, let alone how they could add to zero. Is there some context here that you aren't showing?

View attachment 82589
So to find the equation of family of circles touching line L at point P(p,q), can i use the same equation taking S to be a circle of radius zero and center at P?
That is, if L is ax+by+c=0 and P is (p,q), then S will be $(x-p)^2+(y-q)^2=0$ and the equation of family of circles will be $(x-p)^2+(y-q)^2+\lambda (ax+by+c)=0$. Is this correct? such a circle passes through P.

Your image doesn't show any coordinate system, but your equations here assume that there is one. Is the line vertical? If so, its equation will be x = k for some constant k.

If the radius of your circle is 0 and its center is at (p, q), this is a degenerate circle (a single point). Note that if $(x-p)^2+(y-q)^2=0$, then the only solution is x = p, y = q.

I don't understand where this equation comes from: $(x-p)^2+(y-q)^2+\lambda (ax+by+c)=0$.

 

[AdityaDev]

As it stands, this equation doesn't make sense to me. I don't know what it means to add a circle and a multple of a line, let alone how they could add to zero. Is there some context here that you aren't showing?

Your image doesn't show any coordinate system, but your equations here assume that there is one. Is the line vertical? If so, its equation will be x = k for some constant k.

I have gone through coordinate geometry by S.L.Loney and I found the same thing.
The equation of any curve passing through the points of intersection of a given curve S and line L is S+kL=0.
This equation is correct because the resultant equation passes through the two points of intersection.
Similarly, the equation of a circle passing through the angular points of a quadrilateral whose side equations are $L_1,L_2,L_3,L_4$ is given by
$L_1L_2+\lambda L_3L_4=0$
Lambda is a parameter. Its not a vertical line. Its just a rough diagram.
Yes. They add to zero when you substitute the point of contact of the given circle and the line. This is how the family of circles is specified. They all have to touch that point.

 

[Mark44]

I have gone through coordinate geometry by S.L.Loney and I found the same thing.
The equation of any curve passing through the points of intersection of a given curve S and line L is S+kL=0.

As a guess, this equation is some notation whose meaning is not obvious to someone without the book you cited. It is no mathematically meaningful to "add" a circle and a multiple of a line.

This equation is correct because the resultant equation passes through the two points of intersection.

An equation doesn't pass through points -- it is not a geometric object. A given point can satisfy an equation (i.e., make the equation a true statement).

Similarly, the equation of a circle passing through the angular points of a quadrilateral whose side equations are $L_1,L_2,L_3,L_4$ is given by
$L_1L_2+\lambda L_3L_4=0$
Lambda is a parameter. Its not a vertical line. Its just a rough diagram.

Again, I don't see how this makes sense, unless it is notation that is not to be taken literally. If, as you say, L₁ is an equation, then it's not something that can be used in an arithmetic expression.

Here's an example.
Let E₁ be the equation 2x + 3y = 5
Let E₂ be the equation x²y = 1
How is E₁E₂ meaningful? We would have (2x + 3y = 5)(x²y + 3y = 1). I have never seen any mathematics text talk about multiplying one equation by another.

Yes. They add to zero when you substitute the point of contact of the given circle and the line. This is how the family of circles is specified. They all have to touch that point.

To get back to what you originally asked about, let me make a simplifying assumption; namely, that line L is vertical, and its equation is x = p. If C is any circle that touches the point (p, q) and whose radius is r, then its center must be at (p + r, q). The center of the circle has to be on a horizontal line that intersections the vertical line at (p, q).

The equation of the circle would be $(x - (p + r))^2 + (y - q)^2 = r^2$. Note that if r = 0, this equation simplifies to $(x - p)^2 + (y - q)^2 = 0$, and we get only the point (p, q). Also, if we allow r to be negative, we get circles on the other side of the vertical line. In this case, we would take the radius of the circle to be |r|.