btb4198
- 570
- 10
I need an equation to graph a sine wave that act like a unit circle but only positive numbers.
so I need it to be 0 at 0, A at 90 , 0 at 180, A at 270, 0 at 360, and A at 450 and so on and so on...
Now I know sin(0) is 0 in degrees and sin(90) 1
and I know if you Square a number is will always get you a positive number
so Y = A* sin(x)^2 should work, but x has to be in degrees, so you have to convert from radians to degrees.
with is 180/π
so now I have
Y = A * sin(x*(180/π) ^2
but this is not working on my computer's graphing Calculator:
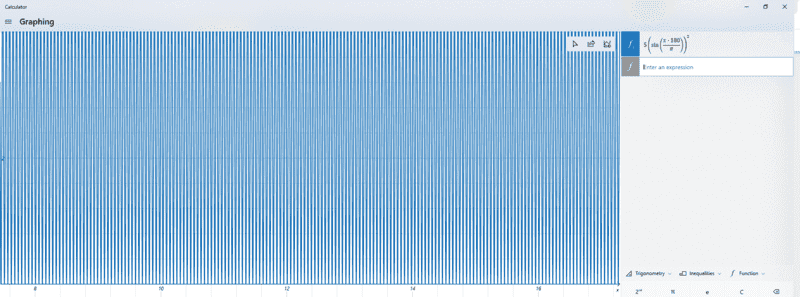
I made A = 5
I tried doing adding - 90
Y = A * sin(x*(180/π -90) ^2
but that did not work
I never trying adding 90, - 360 and 360 nothing is working.
why is this ? what am I missing ?
ago the graph should be 0 on 0, 180 , and 360 and should be A( in this case 5) only on 90, 270 and 450 and so on and so on
so I need it to be 0 at 0, A at 90 , 0 at 180, A at 270, 0 at 360, and A at 450 and so on and so on...
Now I know sin(0) is 0 in degrees and sin(90) 1
and I know if you Square a number is will always get you a positive number
so Y = A* sin(x)^2 should work, but x has to be in degrees, so you have to convert from radians to degrees.
with is 180/π
so now I have
Y = A * sin(x*(180/π) ^2
but this is not working on my computer's graphing Calculator:
I made A = 5
I tried doing adding - 90
Y = A * sin(x*(180/π -90) ^2
but that did not work
I never trying adding 90, - 360 and 360 nothing is working.
why is this ? what am I missing ?
ago the graph should be 0 on 0, 180 , and 360 and should be A( in this case 5) only on 90, 270 and 450 and so on and so on
Last edited by a moderator: