Equilateral Triangle Intersecting Lines Theorem

[anemone]

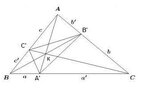
Let $ABC$ be an equilateral triangle, and let $K$ be a point in its interior. Let the line $AK,\,BK,\,CK$ meet the sides of $BC,\,CA,\,AB$ in the points $A',\,B',\,C'$ respectively. Prove that

$A'B'\cdot B'C'\cdot C'A' \ge A'B\cdot B'C\cdot C'A$.

 

[anemone]

Solution of other:

Spoiler

View attachment 3052

Let $A'B=a,\,A'C=a',\,B'C=b,\,B'A=b',\,C'A=c$ and $C'B=c'$. Then by Ceva's Theorem, we have $abc=a'b'c'$---(*).

Since $\angle B'AC'=60^{\circ}$, we have

$\begin{align*}B'C'^2&=(b')^2+c^2-2b'c\cos 60^{\circ}\\&=(b')^2+c^2-b'c\ge b'c\end{align*}$

Similarly we have

$C'A'\ge c'a$ and $A'B'^2\ge a'b$

Multiplying these three inequalities, we get

$B'C'^2\cdot C'A'^2\cdot A'B'^2\ge b'c\cdot c'a \cdot a'b$---(**)

From (*) and (**) we have $B'C'^2\cdot C'A'^2\cdot A'B'^2 \ge a^2b^2c^2$

Thus we have $B'C'\cdot C'A'\cdot A'B' \ge abc$

That is, $A'B'\cdot B'C'\cdot C'A' \ge A'B\cdot B'C\cdot C'A$.